In mathematics the Legendre rational functions are a sequence of orthogonal functions on [0, ∞). They are obtained by composing the Cayley transform with Legendre polynomials.
A rational Legendre function of degree n is defined as:
R n ( x ) = 2 x + 1 L n ( x − 1 x + 1 ) where L n ( x ) is a Legendre polynomial. These functions are eigenfunctions of the singular Sturm-Liouville problem:
( x + 1 ) ∂ x ( x ∂ x ( ( x + 1 ) v ( x ) ) ) + λ v ( x ) = 0 with eigenvalues
λ n = n ( n + 1 ) Many properties can be derived from the properties of the Legendre polynomials of the first kind. Other properties are unique to the functions themselves.
R n + 1 ( x ) = 2 n + 1 n + 1 x − 1 x + 1 R n ( x ) − n n + 1 R n − 1 ( x ) f o r n ≥ 1 and
2 ( 2 n + 1 ) R n ( x ) = ( x + 1 ) 2 ( ∂ x R n + 1 ( x ) − ∂ x R n − 1 ( x ) ) + ( x + 1 ) ( R n + 1 ( x ) − R n − 1 ( x ) ) It can be shown that
lim x → ∞ ( x + 1 ) R n ( x ) = 2 and
lim x → ∞ x ∂ x ( ( x + 1 ) R n ( x ) ) = 0 ∫ 0 ∞ R m ( x ) R n ( x ) d x = 2 2 n + 1 δ n m where δ n m is the Kronecker delta function.
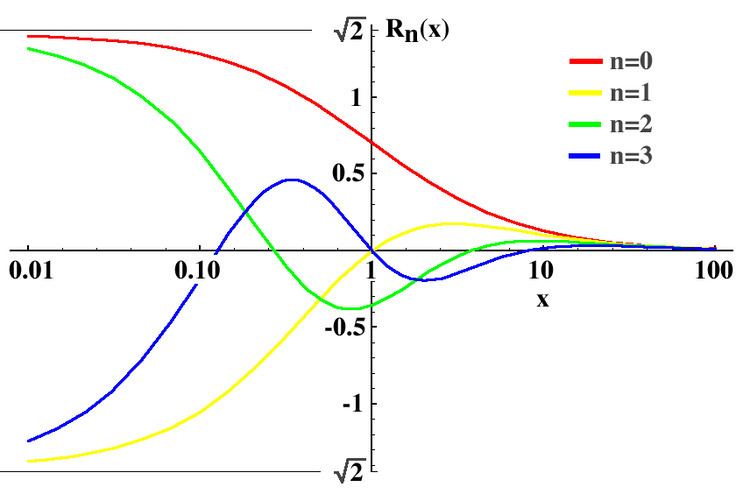
R 0 ( x ) = 1 R 1 ( x ) = x − 1 x + 1 R 2 ( x ) = x 2 − 4 x + 1 ( x + 1 ) 2 R 3 ( x ) = x 3 − 9 x 2 + 9 x − 1 ( x + 1 ) 3 R 4 ( x ) = x 4 − 16 x 3 + 36 x 2 − 16 x + 1 ( x + 1 ) 4