Legendre function

Differential equation

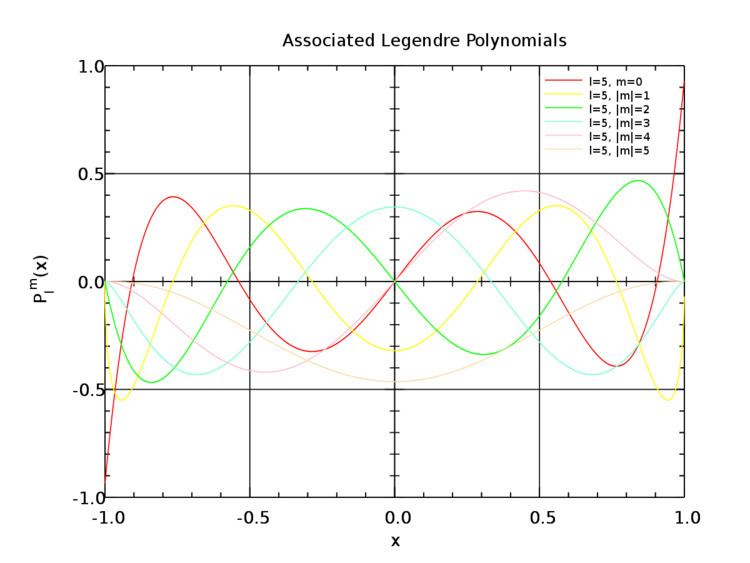
Associated Legendre functions are solutions of the general Legendre equation

( 1 − x 2 ) y ″ − 2 x y ′ + [ λ ( λ + 1 ) − μ 2 1 − x 2 ] y = 0 ,

where the complex numbers λ and μ are called the degree and order of the associated Legendre functions, respectively. The Legendre polynomials are the associated Legendre functions of order μ=0.

This is a second order linear equation with three regular singular points (at 1, −1, and ∞). Like all such equations, it can be converted into a hypergeometric differential equation by a change of variable, and its solutions can be expressed using hypergeometric functions.

Definition

These functions may actually be defined for general complex parameters and argument:

P λ μ ( z ) = 1 Γ ( 1 − μ ) [ 1 + z 1 − z ] μ / 2 2 F 1 ( − λ , λ + 1 ; 1 − μ ; 1 − z 2 ) , for    | 1 − z | < 2

where Γ is the gamma function and 2 F 1 is the hypergeometric function.

The second order differential equation has a second solution, Q λ μ ( z ) , defined as:

Q λ μ ( z ) = π   Γ ( λ + μ + 1 ) 2 λ + 1 Γ ( λ + 3 / 2 ) e i μ π ( z 2 − 1 ) μ / 2 z λ + μ + 1 2 F 1 ( λ + μ + 1 2 , λ + μ + 2 2 ; λ + 3 2 ; 1 z 2 ) , for     | z | > 1. A useful relation between Legendre P and Q functions is Whipple's formula.

Integral representations

The Legendre functions can be written as contour integrals. For example,

P λ ( z ) = P λ 0 ( z ) = 1 2 π i ∫ 1 , z ( t 2 − 1 ) λ 2 λ ( t − z ) λ + 1 d t

where the contour winds around the points 1 and z in the positive direction and does not wind around −1. For real x, we have

P s ( x ) = 1 2 π ∫ − π π ( x + x 2 − 1 cos ⁡ θ ) s d θ = 1 π ∫ 0 1 ( x + x 2 − 1 ( 2 t − 1 ) ) s d t t ( 1 − t ) , s ∈ C

Legendre function as characters

The real integral representation of P s are very useful in the study of harmonic analysis on L 1 ( G / / K ) where G / / K is the double coset space of S L ( 2 , R ) (see Zonal spherical function). Actually the Fourier transform on L 1 ( G / / K ) is given by

L 1 ( G / / K ) ∋ f ↦ f ^

where

f ^ ( s ) = ∫ 1 ∞ f ( x ) P s ( x ) d x , − 1 ≤ ℜ ( s ) ≤ 0