Lattice reduction

Nearly Orthogonal

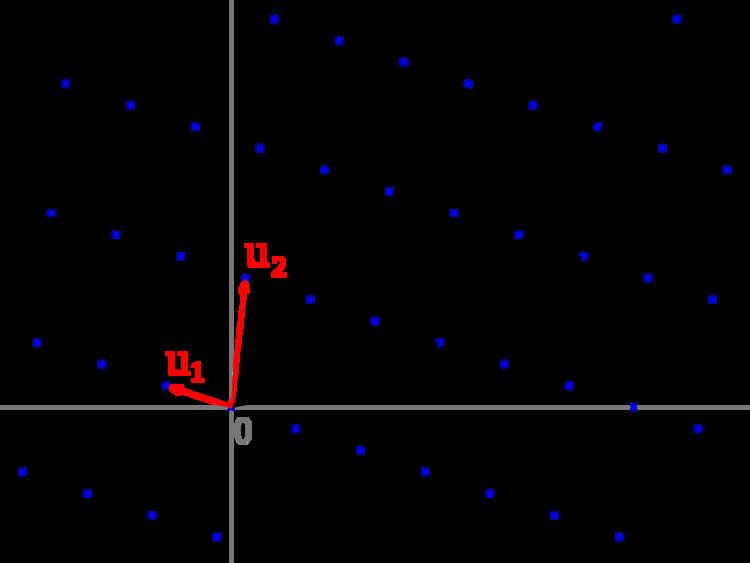
One measure of nearly orthogonal is the orthogonality defect. This compares the product of the lengths of the basis vectors with the volume of the parallelepiped they define. For perfectly orthogonal basis vectors, these quantities would be the same.

Any particular basis of n vectors may be represented by a matrix B , whose columns are the basis vectors b i , i = 1 , … , n . In the fully dimensional case where the number of basis vectors is equal to the dimension of the space they occupy, this matrix is square, and the volume of the fundamental parallelepiped is simply the absolute value of the determinant of this matrix det ( B ) . If the number of vectors is less than the dimension of the underlying space, then volume is det ( B T B ) . For a given lattice Λ , this volume is the same (up to sign) for any basis, and hence is referred to as the determinant of the lattice det ( Λ ) or lattice constant d ( Λ ) .

The orthogonality defect is the product of the basis vector lengths divided by the parallelepiped volume;

From the geometric definition it may be appreciated that δ ( B ) ≥ 1 with equality if and only if the basis is orthogonal.

If the lattice reduction problem is defined as finding the basis with the smallest possible defect, then the problem is NP complete. However, there exist polynomial time algorithms to find a basis with defect δ ( B ) ≤ c where c is some constant depending only on the number of basis vectors and the dimension of the underlying space (if different). This is a good enough solution in many practical applications.

In two dimensions

For a basis consisting of just two vectors, there is a simple and efficient method of reduction closely analogous to the Euclidean algorithm for the greatest common divisor of two integers. As with the Euclidean algorithm, the method is iterative; at each step the larger of the two vectors is reduced by adding or subtracting an integer multiple of the smaller vector.

Applications

Lattice reduction algorithms are used in a number of modern number theoretical applications, including in the discovery of a spigot algorithm for π . Although determining the shortest basis is possibly an NP-complete problem, algorithms such as the LLL algorithm can find a short (not necessarily shortest) basis in polynomial time with guaranteed worst-case performance. LLL is widely used in the cryptanalysis of public key cryptosystems.

When used to find integer relations, a typical input to the algorithm consists of an augmented n x n identity matrix with the entries in the last column consisting of the n elements (multiplied by a large positive constant w to penalize vectors that do not sum to zero) between which the relation is sought.

The LLL algorithm for computing a nearly-orthogonal basis was used to show that integer programming in any fixed dimension can be done in polynomial time.

Algorithms

The following algorithms reduce lattice bases. They can be compared in terms of runtime and approximation to an optimal solution, always relative to the dimension of the given lattice. If there are public implementations of these algorithms this should also be noted here.