Lattice (discrete subgroup)

Informal discussion

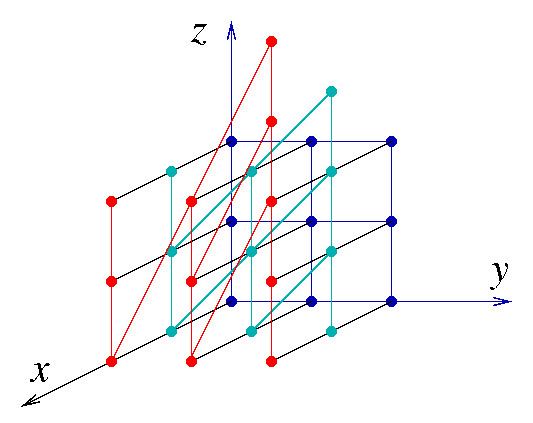
Lattices are best thought of as discrete approximations of continuous groups (such as Lie groups). For example, it is intuitively clear that the subgroup Z n of integer vectors "looks like" the real vector space R n in some sense, while both groups are essentially different: one is finitely generated and countable, while the other is not (as a group) and has the cardinality of the continuum.

Rigorously defining the meaning of "approximation of a continuous group by a discrete subgroup" in the previous paragraph in order to get a notion generalising the example Z n ⊂ R n is a matter of what it is designed to achieve. Maybe the most obvious idea is to say that a subgroup "approximates" a larger group is that the larger group can be covered by the translates of a "small" subset by all elements in the subgroups. In a locally compact topological group there are two immediately available notions of "small": topological (a compact, or relatively compact subset) or measure-theoretical (a subset of finite Haar measure). Note that since the Haar measure is a Borel measure, in particular gives finite mass to compact subsets, the second definition is more inclusive. The definition of a lattice used in mathematics relies upon the second meaning (in particular to include such examples as S L 2 ( Z ) ⊂ S L 2 ( R ) ) but the first also has its own interest (such lattices are called uniform).

Definition

Let G be a locally compact group and Γ a discrete subgroup (this means that there exists a neighbourhood U of the identity element e G of G such that Γ ∩ U = { e G } ). Then Γ is called a lattice in G if in addition there exists a Borel measure μ on the quotient space G / Γ which is finite (i.e. μ ( G / Γ ) < + ∞ ) and G -invariant (meaning that for any g ∈ G and any open subset W ⊂ G / Γ the equality μ ( g W ) = μ ( W ) is satisifed).

A slightly more sophisticated formulation is as follows: suppose in addition that G is unimodular, then since Γ is discrete it is also unimodular and by general theorems there exists a unique G -invariant Borel measure on G / Γ up to scaling. Then Γ is a lattice if and only if this measure is finite.

In the case of discrete subgroups this invariant measure coincides locally with the Haar measure and hence a discrete subgroup in a locally compact group G being a lattice is equivalent to it having a fundamental domain (for the action on G by left-translations) of finite volume for the Haar measure.

A lattice Γ ⊂ G is called uniform when the quotient space G / Γ is compact (and non-uniform otherwise). Equivalently a discrete subgroup Γ ⊂ G is a uniform lattice if and only if there exists a compact subset C ⊂ G with G = ⋃ γ ∈ Γ C γ . Note that if Γ is any discrete subgroup in G such that G / Γ is compact then Γ is automatically a lattice in G .

First examples

The fundamental, and simplest, example is the subgroup Z n which is a lattice in the Lie group R n . A slightly more complicated example is given by the discrete Heisenberg group inside the continuous Heisenberg group.

If G is a discrete group then a lattice in G is exactly a subgroup Γ of finite index (i.e. the quotient set G / Γ is finite).

All of these examples are uniform. A non-uniform example is given by the modular group S L 2 ( Z ) inside S L 2 ( R ) , and also by the higher-dimensional analogues S L n ( Z ) ⊂ S L n ( R ) .

Any finite-index subgroup of a lattice is also a lattice in the same group. More generally, a subgroup commensurable to a lattice is a lattice.

Which groups have lattices?

Not every locally compact group contains a lattice, and there is no general group-theoretical sufficient condition for this. On the other hand, there are plenty of more specific settings where such criteria exist. For example, the existence or non-existence of lattices in Lie groups is a well-understood topic.

As we mentioned, a necessary condition for a group to contain a lattice is that it be unimodular. This allows for the easy construction of groups without lattices, for example the group of invertible upper triangular matrices or the affine groups. It is also not very hard to find unimodular groups without lattices, for example certain nilpotent Lie groups as explained below.

A stronger condition than unimodularity is simplicity. This is sufficient to imply the existence of a lattice in a Lie group, but in the more general setting of locally compact groups there exists simple groups without lattices, for example the "Neretin groups".

Nilpotent Lie groups

For nilpotent groups the theory simplifies much from the general case, and stays similar to the case of Abelian groups. All lattices in a nilpotent Lie group are uniform, and if N is a connected simply connected Lie group (equivalently it does not contain a nontrivial compact subgroup) then a discrete subgroup is a lattice if and only if it is not contained in a proper connected subgroup (this generalises the fact that a discrete subgroup in a vector space is a lattice if and only if it spans the vector space).

A nilpotent Lie group contains a lattice if and only if it can be defined over the rationals, that is if and only if its structure constants are rational numbers. In particular any nilpotent Lie algebra with irrational structure constants is an example of an unimodular group without a lattice. More precisely, in a nilpotent group satisfying this condition lattices correspond via the exponential map to lattices (in the more elementary sense of Lattice (group)) in the Lie algebra.

A lattice in a nilpotent Lie group N is always finitely generated (and hence finitely presented since it is itself nilpotent); in fact it is generated by at most dim ⁡ ( N ) elements.

Finally, a nilpotent group is isomorphic to a lattice in a nilpotent Lie group if and only if it contains a subgroup of finite index which is torsion-free and of finitely generated.

The general case

The criterion for nilpotent Lie groups to have a lattice given above does not apply to more general solvable Lie groups. It remains true that any lattice in a solvable Lie group is uniform and that lattices in solvable groups are finitely presented.

Not all finitely generated solvable groups are lattices in a Lie group. An algebraic criterion is that the group be polycyclic.

Arithmetic groups and existence of lattices

If G is a semisimple linear algebraic group in G L n ( R ) which is defined over the field Q of rational numbers (i.e. the polynomial equations defining G have their coefficients in Q ) then it has a subgroup Γ = G ∩ G L n ( Z ) . A fundamental theorem of Armand Borel and Harish-Chandra states that Γ is always a lattice in G ; the simplest example of this is the subgroup S L 2 ( Z ) ⊂ S L 2 ( R ) .

Generalising the construction above one gets the notion of an arithmetic lattice in a semisimple Lie group. Since all semisimple Lie groups can be defined over Q a consequence of the arithmetic construction is that any semisimple Lie group contains a lattice.

Irreducibility

When the Lie group G splits as a product G = G 1 × G 2 there is an obvious construction of lattices in G from the smaller groups: if Γ 1 ⊂ G 1 , Γ 2 ⊂ G 2 are lattices then Γ 1 × Γ 2 ⊂ G is a lattice as well. Roughly, a lattice is then said to be irreducible if it does not come from this construction.

More formally, if G = G 1 × … × G r is the decomposition of G into simple factors, a lattice Γ ⊂ G is said to be irreducible if either of the following equivalent conditions hold:

An example of an irreducible lattice is given by the subgroup S L 2 ( Z [ 2 ] ) which we view as a subgroup S L 2 ( R ) × S L 2 ( R ) via the map g ↦ ( g , σ ( g ) ) where σ is the Galois map sending a matric with coefficients a i + b i 2 to a i − b i 2 .

Rank 1 versus higher rank

The real rank of a Lie group is the maximal dimension of an abelian subgroup containing only semisimple elements. The semisimple Lie groups of real rank 1 without compact factors are (up to isogeny) those in the following list (see List of simple Lie groups):

The real rank of a Lie group has a significant influence on the behaviour of the lattices it contains. In particularn the behaviour of lattices in the first two families of groups (and to a lesser extent that of lattices in the latter two) differs much from that of irreducible lattices in groups of higher rank. For example:

Kazhdan's property (T)

The property known as (T) was introduced by Kazhdan to study the algebraic structure lattices in certain Lie groups when the classical, more geometric methods failed or at least were not as efficient. The fundamental result when studying lattices is the following:

Using harmonic analysis it is possible to classify semisimple Lie groups according to whether or not they have the property. As a consequence we get the following result, further illustrating the dichotomy of the previous section:

Finiteness properties

Lattices in semisimple Lie groups are always finitely presented. For uniform lattices this is a direct consequence of cocompactness. In the non-uniform case this can be proved using reduction theory. However a much faster proof is by using Kazhdan's property (T) when possible.

Left-invariant metrics

If G is a Lie group then from an inner product g e on the tangent space g (the Lie algebra of G ) one can construct a Riemannian metric on G as follows: if v , w belong to the tangent space at a point γ ∈ G put g γ ( v , w ) = g e ( γ ∗ v , γ ∗ w ) where γ ∗ indicates the tangent map (at γ ) of the diffeomorphism x ↦ γ − 1 x of G .

The maps x ↦ γ x for γ ∈ G are by definition isometries for this metric g . In particular, if Γ is any discrete subgroup in G (so that it acts freely and properly discontinuously by left-translations on G ) the quotient Γ ∖ G is a Riemannian manifold locally isometric to G with the metric g .

The Riemannian volume form associated to g defines a Haar measure on G and we see that the quotient manifold is of finite Riemannian volume if and only if Γ is a lattice.

Interesting examples in this class of Riemannian spaces include compact flat manifolds and nilmanifolds.

Locally symmetric spaces

A natural inner product on g is given by the Killing form. If G is not compact it is not definite and hence not an inner product: however when G is semisimple and K is a maximal compact subgroup it can be used to define a G -invariant metric on the homogeneous space X = G / K : such Riemannian manifolds are called symmetric spaces of non-compact type without Euclidean factors.

A subgroup Γ ⊂ G acts freely, properly discontinuously on X if and only if it is discrete and torsion-free. The quotients Γ ∖ X are called locally symmetric spaces. There is thus a bijective correspondence between complete locally symmetric spaces locally isomorphic to X and of finite Riemannian volume, and torsion-free lattices in G . This correspondence can be extended to all lattices by adding orbifolds on the geometric side.

Lattices in p-adic Lie groups

A class of groups with similar properties (with respect to lattices) to real semisimple Lie groups are semisimple algebraic groups over local fields of characteristic 0, for example the p-adic fields Q p . There is an arithmetic construction similar to the real case, and the dichotomy between higher rank and rank one also holds in this case, in a more marked form. Let G be an algebraic group over Q p of split- Q p -rank r. Then:

In the latter case all lattices are in fact free groups (up to finite index).

S-arithmetic groups

More generally one can look at lattices in groups of the form

where G p is a semisimple algebraic group over Q p . Usually p = ∞ is allowed, in which case G ∞ is a real Lie group. An example of such a lattice is given by

This arithmetic construction can be generalised to obtain the notion of an S-arithmetic group. The Margulis arithmeticity theorem applies to this setting as well. In particular, if at least two of the factors G p are noncompact then any irreducible lattice in G is S-arithmetic.

Lattices in adelic groups

If G is a semisimple algebraic group over a number field F and A its adèle ring then the group G = G ( A ) of adélic points is well-defined (modulo some technicalities) and it is a locally compact group which naturally contains the group G ( F ) of F -rational point as a discrete subgroup. The Borel–Harish-Chandra theorem extends to this setting, and G ( F ) ⊂ G ( A ) is a lattice.

The strong approximation theorem relates the quotient G ( F ) ∖ G ( A ) to more classical S-arithmetic quotients. This fact makes the adèle groups very effective as tools in the theory of automorphic forms. In particular modern forms of the trace formula are usually stated and proven for adélic groups rather than for Lie groups.

Rigidity results

Another group of phenomena concerning lattices in semisimple algebraic groups is collectively known as rigidity. Here are three classical examples of results in this category.

Local rigidity results state that in most situations every subgroup which is sufficiently "close" to a lattice (in the intuitive sense, formalised by Chabauty topology) is actually conjugated to the original lattice by an element of the ambient Lie group. A consequence of local rigidity and the Kazhdan-Margulis theorem is Wang's theorem: in a given group (with a fixed Haar measure), for any v>0 there are only finitely many (up to conjugation) lattices with covolume bounded by v.

The Mostow rigidity theorem states that for lattices in simple Lie groups not locally isomorphic to S L 2 ( R ) (the group of 2 by 2 matrices with determinant 1) any isomorphism of lattices is essentially induced by an isomorphism between the groups themselves. In particular, a lattice in a Lie group "remembers" the ambient Lie group through its group structure. The first statement is sometimes called strong rigidity and is due to George Mostow and Gopal Prasad (Mostow proved it for cocompact lattices and Prasad extended it to the general case).

Superrigidity provides (for Lie groups and algebraic groups over local fields of higher rank) a generalization dealing with homomorphisms from a lattice in an algebraic group G into another algebraic group H. It was proven by Grigori Margulis and is an essential ingredient in the proof of his arithmeticity theorem.

Nonrigidity in low dimensions

The only groups for which Mostow rigidity does not hold are all groups locally isomorphic to P S L 2 ( R ) . In this case there are in fact continuously many lattices and they give rise to Teichmüller spaces.

Nonuniform lattices in the group P S L 2 ( C ) are not locally rigid. In fact they are accumulation points (in the Chabauty topology) of lattices of smaller covolume, as demonstrated by hyperbolic Dehn surgery.

As lattices in rank-one p-adic groups are virtually free groups they are very non-rigid.

Definition

Let T be a tree with a cocompact group of automorphisms; for example, T can be a regular or biregular tree. The group of automorphisms A u t ( T ) of T is a locally compact group (when endowed with the compact-open topology, in which a basis of neighbourhoods of the identity is given by the stabilsers of finite subtrees, which are compact). Any group which is a lattice in some A u t ( T ) is then called a tree lattice.

The discreteness in this case is easy to see from the group action on the tree: a subgroup of A u t ( T ) is discrete if and only if all vertex stabilisers are finite groups.

It is easily seen from the basic theory of group actions on trees that uniform tree lattices are virtually free groups. Thus the more interesting tree lattices are the non-uniform ones, equivalently those for which the quotient graph Γ ∖ T is infinite. The existence of such lattices is not easy to see.

Tree lattices from algebraic groups

If F is a local field of positive characteristic (i.e. a completion of a function field of a curve over a finite field, for example the field of formal Laurent power series F p ( ( t ) ) ) and G an algebraic group defined over F of F -split rank one, then any lattice in G is a tree lattice through its action on the Bruhat-Tits building which in this case is a tree. In contrast to the characteristic 0 case such lattices can be nonuniform, and in this case they are never finitely generated.

Tree lattices from Bass-Serre theory

If Γ is the fundamental group of an infinite graph of groups, all of whose vertex groups are finite, and under additional necessary assumptions on the index of the edge groups and the size of the vertex groups, then the action of Γ on the Bass-Serre tree associated to the graph of groups realises it as a tree lattice.

Existence criterion

More generally one can ask the following question: if H is a closed subgroup of A u t ( T ) , under which conditions does H < / m a t > H contain a lattice? The existence of a uniform lattice is equivalent to H being unimodular and the quotient H ∖ T being finite. The general existence theorem is more subtle: it is necessary and sufficient that H be unimodular, and that the quotient H ∖ T be of "finite volume" in a suitable sense (which can be expressed combinatorially in terms of the action of H ), more general than the stroger condition that the quotient be finite (as proven by the very existence of nonuniform tree lattices).