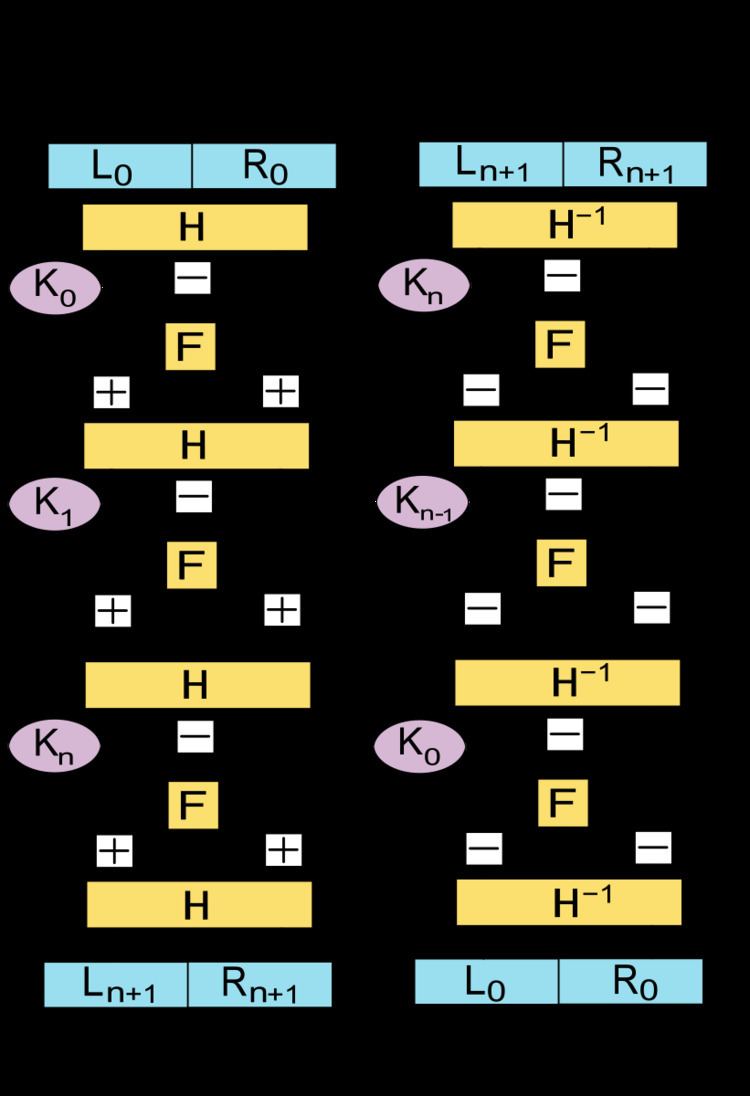
The Lai-Massey scheme is a cryptographic structure used in the design of block ciphers. It is used in IDEA and IDEA NXT.
Let
F
be the round function and
H
a half-round function and let
K
0
,
K
1
,
…
,
K
n
be the sub-keys for the rounds
0
,
1
,
…
,
n
respectively.
Then the basic operation is as follows:
Split the plaintext block into two equal pieces, (
L
0
,
R
0
)
For each round
i
=
0
,
1
,
…
,
n
, compute
(
L
i
+
1
′
,
R
i
+
1
′
)
=
H
(
L
i
′
+
T
i
,
R
i
′
+
T
i
)
where
T
i
=
F
(
L
i
′
−
R
i
′
,
K
i
)
and
(
L
0
′
,
R
0
′
)
=
H
(
L
0
,
R
0
)
Then the ciphertext is
(
L
n
+
1
,
R
n
+
1
)
=
(
L
n
+
1
′
,
R
n
+
1
′
)
.
Decryption of a ciphertext
(
L
n
+
1
,
R
n
+
1
)
is accomplished by computing for
i
=
n
,
n
−
1
,
…
,
0
(
L
i
′
,
R
i
′
)
=
H
−
1
(
L
i
+
1
′
−
T
i
,
R
i
+
1
′
−
T
i
)
where
T
i
=
F
(
L
i
+
1
′
−
R
i
+
1
′
,
K
i
)
and
(
L
n
+
1
′
,
R
n
+
1
′
)
=
H
−
1
(
L
n
+
1
,
R
n
+
1
)
Then
(
L
0
,
R
0
)
=
(
L
0
′
,
R
0
′
)
is the plaintext again.
The Lai-Massey scheme offers security properties similar to those of the Feistel structure. It also shares its advantage over a substitution-permutation network that the round function
F
does not have to be invertible.
The half-round function is required to prevent a trivial distinguishing attack (
L
0
−
R
0
=
L
n
+
1
−
R
n
+
1
). It commonly applies an orthomorphism
σ
on the left hand side, that is,
H
(
L
,
R
)
=
(
σ
(
L
)
,
R
)
where both
σ
and
x
↦
σ
(
x
)
−
x
are permutations (in the mathematical sense, that is, a bijection – not a permutation box). Since there are no orthomorphisms for bit blocks (groups of size
2
n
), "almost orthomorphisms" are used instead.
H
may depend on the key. If it doesn't, the last application can be omitted, since its inverse is known anyway. The last application is commonly called "round
n
.5
" for a cipher that otherwise has
n
rounds.
X. Lai. On the design and security of block ciphers. ETH Series in Information Processing, vol. 1, Hartung-Gorre, Konstanz, 1992
X. Lai, J. L. Massey. A proposal for a new block encryption standard. Advances in Cryptology EUROCRYPT'90, Aarhus, Denmark, LNCS 473, p. 389-404, Springer, 1991
Serge Vaudenay: A Classical Introduction to Cryptography, p. 33