Harman Patil (Editor)

Lah number

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Lah number

In mathematics, the Lah numbers, discovered by Ivo Lah in 1955, are coefficients expressing rising factorials in terms of falling factorials.

Contents

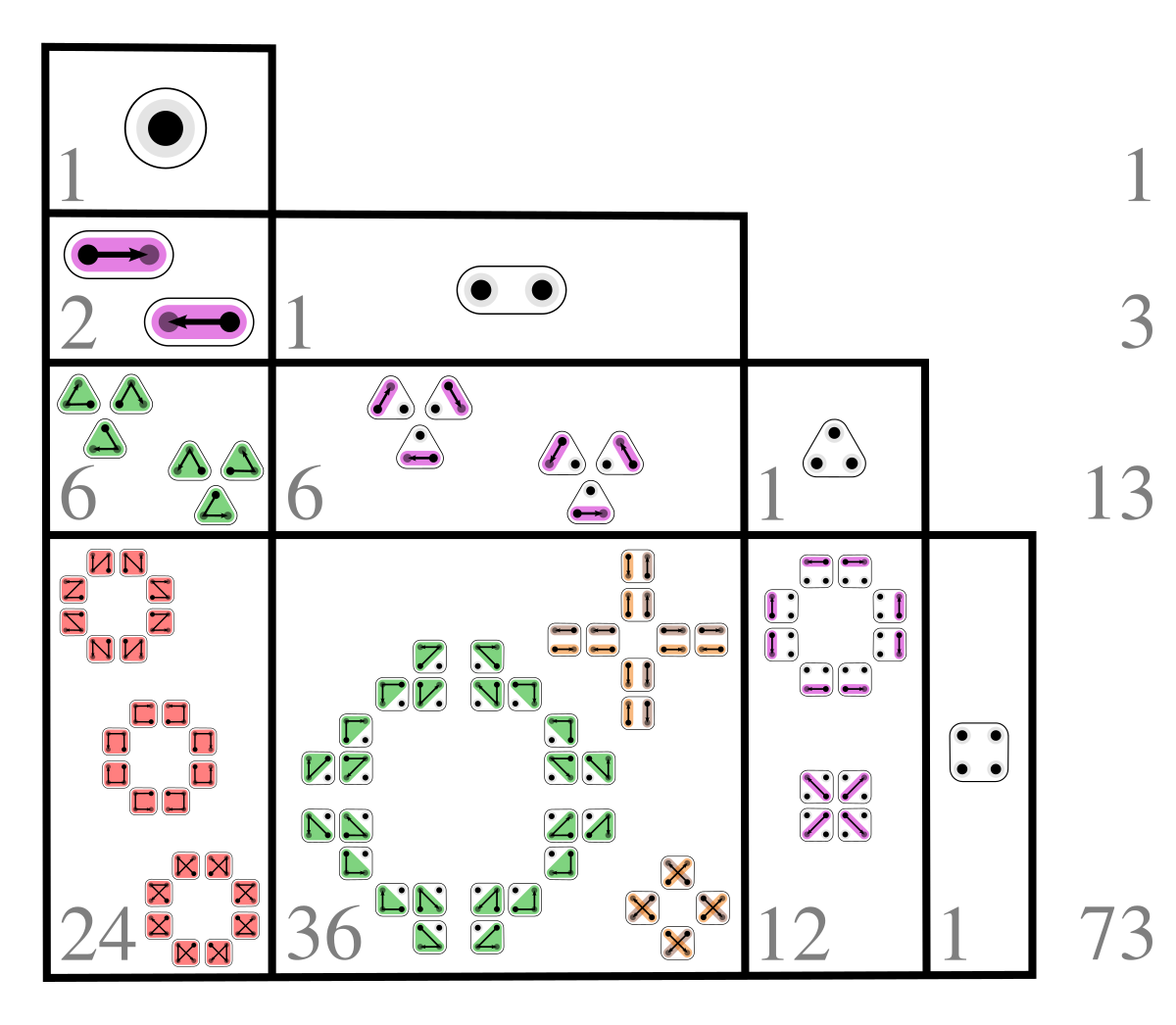
Unsigned Lah numbers have an interesting meaning in combinatorics: they count the number of ways a set of n elements can be partitioned into k nonempty linearly ordered subsets. Lah numbers are related to Stirling numbers.

Unsigned Lah numbers (sequence A105278 in the OEIS):

L ( n , k ) = ( n − 1 k − 1 ) n ! k ! .

Signed Lah numbers (sequence A008297 in the OEIS):

L ′ ( n , k ) = ( − 1 ) n ( n − 1 k − 1 ) n ! k ! .

L(n, 1) is always n!; in the interpretation above, the only partition of {1, 2, 3} into 1 set can have its set ordered in 6 ways:

{(1, 2, 3)}, {(1, 3, 2)}, {(2, 1, 3)}, {(2, 3, 1)}, {(3, 1, 2)} or {(3, 2, 1)}

L(3, 2) corresponds to the 6 partitions with two ordered parts:

{(1), (2, 3)}, {(1), (3, 2)}, {(2), (1, 3)}, {(2), (3, 1)}, {(3), (1, 2)} or {(3), (2, 1)}

L(n, n) is always 1 since, e.g., partitioning {1, 2, 3} into 3 non-empty subsets results in subsets of length 1.

{(1), (2), (3)}

Adapting the Karamata–Knuth notation for Stirling numbers, it has been proposed to use the following alternative notation for Lah numbers:

L ( n , k ) = ⌊ n k ⌋ .

Rising and falling factorials

Let x ( n ) represent the rising factorial x ( x + 1 ) ( x + 2 ) ⋯ ( x + n − 1 ) and let ( x ) n represent the falling factorial x ( x − 1 ) ( x − 2 ) ⋯ ( x − n + 1 ) .

Then x ( n ) = ∑ k = 1 n L ( n , k ) ( x ) k and ( x ) n = ∑ k = 1 n ( − 1 ) n − k L ( n , k ) x ( k ) .

For example, x ( x + 1 ) ( x + 2 ) = 6 x + 6 x ( x − 1 ) + 1 x ( x − 1 ) ( x − 2 ) .

Compare the third row of the table of values.

Identities and relations

L ( n , k ) = ( n − 1 k − 1 ) n ! k ! = ( n k ) ( n − 1 ) ! ( k − 1 ) ! = ( n k ) ( n − 1 k − 1 ) ( n − k ) ! L ( n , k ) = n ! ( n − 1 ) ! k ! ( k − 1 ) ! ⋅ 1 ( n − k ) ! = ( n ! k ! ) 2 k n ( n − k ) ! L ( n , k + 1 ) = n − k k ( k + 1 ) L ( n , k ) . L ( n , k ) = ∑ j [ n j ] { j k } , where [ n j ] are the Stirling numbers of the first kind and { j k } are the Stirling numbers of the second kind, and with the conventions L ( 0 , 0 ) = 1 and L ( n , k ) = 0 if k > n . L ( n , 1 ) = n ! L ( n , 2 ) = ( n − 1 ) n ! / 2 L ( n , 3 ) = ( n − 2 ) ( n − 1 ) n ! / 12 L ( n , n − 1 ) = n ( n − 1 ) L ( n , n ) = 1 ∑ n ≥ k L ( n , k ) x n n ! = 1 k ! ( x 1 − x ) k

Table of values

Below is a table of values for the Lah numbers:

References

Lah number Wikipedia
(Text) CC BY-SA