Laguerre plane

The classical real Laguerre plane

Originally the classical Laguerre plane was defined as the geometry of the oriented lines and circles in the real euclidean plane (see ). Here we prefer the parabola model of the classical Laguerre plane.

We define:

P := R 2 ∪ ( { ∞ } × R ) ,   ∞ ∉ R , the set of points, Z := { { ( x , y ) ∈ R 2 ∣ y = a x 2 + b x + c } ∪ { ( ∞ , a ) } ∣ a , b , c ∈ R } the set of cycles.

The incidence structure ( P , Z , ∈ ) is called classical Laguerre plane.

The point set is R 2 plus a copy of R (see figure). Any parabola/line y = a x 2 + b x + c gets the additional point ( ∞ , a ) .

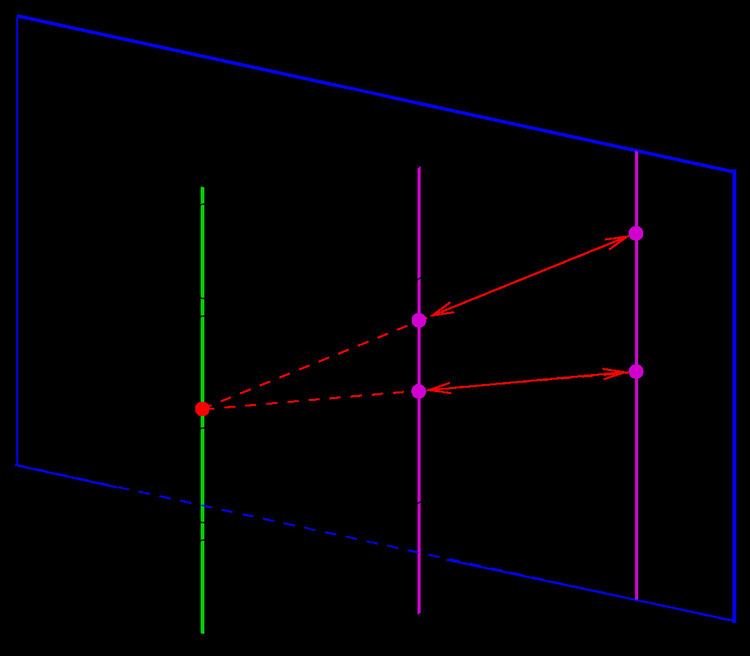
Points with the same x-coordinate cannot be connected by curves y = a x 2 + b x + c . Hence we define:

Two points A , B are parallel ( A ∥ B ) if A = B or there is no cycle containing A and B .

For the description of the classical real Laguerre plane above two points ( a 1 , a 2 ) , ( b 1 , b 2 ) are parallel if and only if a 1 = b 1 . ∥ is an equivalence relation, similar to the parallelity of lines.

The incidence structure ( P , Z , ∈ ) has the following properties:

Lemma:

For any three points A , B , C , pairwise not parallel, there is exactly one cycle z containing A , B , C .

For any point P and any cycle z there is exactly one point P ′ ∈ z such that P ∥ P ′ .

For any cycle z , any point P ∈ z and any point Q ∉ z which is not parallel to P there is exactly one cycle z ′ through P , Q with z ∩ z ′ = { P } , i.e. z and z ′ touch each other at P .

Similar to the sphere model of the classical Moebius plane there is a cylinder model for the classical Laguerre plane:

( P , Z , ∈ ) is isomorphic to the geometry of plane sections of a circular cylinder in R 3 .

The following mapping Φ is a projection with center ( 0 , 1 , 0 ) that maps the x-z-plane onto the cylinder with the equation u 2 + v 2 − v = 0 , axis ( 0 , 1 2 , . . ) and radius r = 1 2   :

Φ :   ( x , z ) → ( x 1 + x 2 , x 2 1 + x 2 , z 1 + x 2 ) = ( u , v , w )   .

The points ( 0 , 1 , a ) (line on the cylinder through the center) appear not as images.

Φ projects the parabola/line with equation z = a x 2 + b x + c into the plane w − a = b u + ( a − c ) ( v − 1 ) . So, the image of the parabola/line is the plane section of the cylinder with a non perpendicular plane and hence a circle/ellipse without point ( 0 , 1 , a ) . The parabolas/line z = a x 2 + a are mapped onto (horizontal) circles.

A line(a=0) is mapped onto a circle/Ellipse through center ( 0 , 1 , 0 ) and a parabola ( a ≠ 0 ) onto a circle/ellipse that do not contain ( 0 , 1 , 0 ) .

The axioms of a Laguerre plane

The Lemma above gives rise to the following definition:

Let L := ( P , Z , ∈ ) be an incidence structure with point set P and set of cycles Z .
Two points A , B are parallel ( A ∥ B ) if A = B or there is no cycle containing A and B .
L is called Laguerre plane if the following axioms hold:

B1: For any three points A , B , C , pairwise not parallel, there is exactly one cycle z which contains A , B , C .B2: For any point P and any cycle z there is exactly one point P ′ ∈ z such that P ∥ P ′ .B3: For any cycle z , any point P ∈ z and any point Q ∉ z which is not parallel to P there is exactly one cycle z ′ through P , Q with z ∩ z ′ = { P } ,i.e. z and z ′ touch each other at P .B4: Any cycle contains at least three points, there is at least one cycle. There are at least four points not on a cycle.

Four points A , B , C , D are concyclic if there is a cycle z with A , B , C , D ∈ z .

From the definition of relation ∥ and axiom B2 we get

Lemma: Relation ∥ is an equivalence relation.

Following the cylinder model of the classical Laguerre-plane we introduce the denotation:

a) For P ∈ P we set P ¯ := { Q ∈ P   |   P ∥ Q } . b) An equivalence class P ¯ is called generator.

For the classical Laguerre plane a generator is a line parallel to the y-axis (plane model) or a line on the cylinder (space model).

The connection to linear geometry is given by the following definition:

For a Laguerre plane L := ( P , Z , ∈ ) we define the local structure

A P := ( P ∖ { P ¯ } , { z ∖ { P ¯ }   |   P ∈ z ∈ Z } ∪ { Q ¯   |   Q ∈ P ∖ { P ¯ } , ∈ )

and call it the residue at point P.

In the plane model of the classical Laguerre plane A ∞ is the real affine plane R 2 . In general we get

Theorem: Any residue of a Laguerre plane is an affine plane.

And the equivalent definition of a Laguerre plane:

Theorem: An incidence structure together with an equivalence relation ∥ on P is a Laguerre plane if and only if for any point P the residue A P is an affine plane.

Finite Laguerre planes

The following incidence structure is a minimal model of a Laguerre plane:

P := { A 1 , A 2 , B 1 , B 2 , C 1 , C 2 }   , Z := { { A i , B j , C k }   |   i , j , k = 1 , 2 }   , A 1 ∥ A 2 ,   B 1 ∥ B 2 ,   C 1 ∥ C 2   .

Hence | P | = 6 and | Z | = 8   .

For finite Laguerre planes, i.e. | P | < ∞ , we get:

Lemma: For any cycles z 1 , z 2 and any generator P ¯ of a finite Laguerre plane L := ( P , Z , ∈ ) we have:

| z 1 | = | z 2 | = | P ¯ | + 1 .

For a finite Laguerre plane L := ( P , Z , ∈ ) and a cycle z ∈ Z the integer n := | z | − 1 is called order of L .

From combinatorics we get

Lemma: Let L := ( P , Z , ∈ ) be a Laguerre—plane of order n . Then

a) any residue A P is an affine plane of order n , b) | P | = n 2 + n , c) | Z | = n 3 .

Miquelian Laguerre planes

Unlike Moebius planes the formal generalization of the classical model of a Laguerre plane, i.e. replacing R by an arbitrary field K , leads in any case to an example of a Laguerre plane.

Theorem: For a field K and

P := K 2 ∪ ( { ∞ } × K ) ,   ∞ ∉ K , Z := { { ( x , y ) ∈ K 2   |   y = a x 2 + b x + c } ∪ { ( ∞ , a ) }   |   a , b , c ∈ K } the incidence structure L ( K ) := ( P , Z , ∈ ) is a Laguerre plane with the following parallel relation: ( a 1 , a 2 ) ∥ ( b 1 , b 2 ) if and only if a 1 = b 1 .

Similar to a Möbius plane the Laguerre version of the Theorem of Miquel holds:

Theorem of MIQUEL: For the Laguerre plane L ( K ) the following is true:

If for any 8 pairwise not parallel points P 1 , … , P 8 which can be assigned to the vertices of a cube such that the points in 5 faces correspond to concyclical quadruples than the sixth quadruple of points is concyclical, too.

(For a better overview in the figure there are circles drawn instead of parabolas)

The importance of the Theorem of Miquel shows the following theorem which is due to v. d. Waerden, Smid and Chen:

Theorem: Only a Laguerre plane L ( K ) satisfies the theorem of Miquel.

Because of the last Theorem L ( K ) is called a miquelian Laguerre plane.

Remark: The minimal model of a Laguerre plane is miquelian.

It is isomorphic to the Laguerre plane L ( K ) with K = G F ( 2 ) (field { 0 , 1 } ).

Remark: A suitable stereographic projection shows: L ( K ) is isomorphic to the geometry of the plane sections on a quadric cylinder over field K .

Ovoidal Laguerre planes

There are a lot of Laguerre planes which are not miquelian (s. weblink below). The class which is most similar to miquelian Laguerre planes are the ovoidal Laguerre planes. An ovoidal Laguerre plane is the geometry of the plane sections of a cylinder which is constructed by using an oval instead of a non degenerate conic. An oval is a quadratic set and bears the same geometric properties as a non degenerate conic in a projective plane: 1) a line intersects an oval in zero, one, or two points and 2) at any point there is a unique tangent. A simple oval in the real plane can be constructed by glueing together two suitable halves of different ellipses, such that the result is not a conic. Even in the finite case there exist ovals (see quadratic set).