 | ||
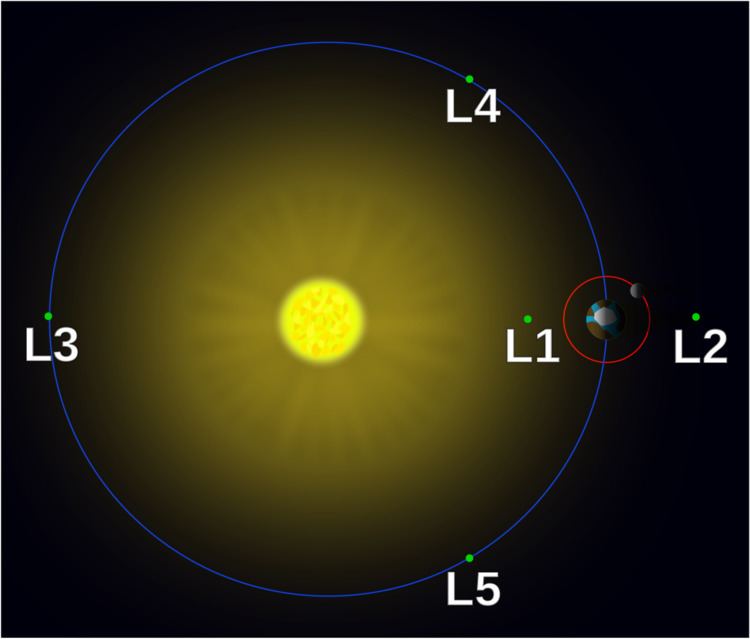
In celestial mechanics, the Lagrangian points (/ləˈɡrɑːndʒiən/; also Lagrange points, L-points, or libration points) are positions in an orbital configuration of two large bodies where a small object affected only by gravity can maintain a stable position relative to the two large bodies. The Lagrange points mark positions where the combined gravitational pull of the two large masses provides precisely the centrifugal force required to orbit with them. There are five such points, labeled L1 to L5, all in the orbital plane of the two large bodies. The first three are on the line connecting the two large bodies; the last two, L4 and L5, each form an equilateral triangle with the two large bodies. The two latter points are stable, which implies that objects can orbit around them in a rotating coordinate system tied to the two large bodies.
Contents
- History
- Lagrange points
- Natural objects at Lagrangian points
- Mathematical details
- L1
- L2
- L3
- L4 and L5
- Stability
- SunEarth
- EarthMoon
- SunVenus
- Spacecraft at SunEarth L1
- Spacecraft at SunEarth L2
- References
Several planets have satellites near their L4 and L5 points (trojans) with respect to the Sun, with Jupiter in particular having more than a million of these. Artificial satellites have been placed at L1 and L2 with respect to the Sun and Earth, and Earth and the Moon, for various purposes, and the Lagrangian points have been proposed for a variety of future uses in space exploration.
History
The three collinear Lagrange points (L1, L2, L3) were discovered by Leonhard Euler a few years before Lagrange discovered the remaining two.
In 1772, Joseph-Louis Lagrange published an "Essay on the three-body problem". In the first chapter he considered the general three-body problem. From that, in the second chapter, he demonstrated two special constant-pattern solutions, the collinear and the equilateral, for any three masses, with circular orbits.
Lagrange points
The five Lagrangian points are labeled and defined as follows:
The L1 point lies on the line defined by the two large masses M1 and M2, and between them. It is the most intuitively understood of the Lagrangian points: the one where the gravitational attraction of M2 partially cancels M1's gravitational attraction.
The L2 point lies on the line through the two large masses, beyond the smaller of the two. Here, the gravitational forces of the two large masses balance the centrifugal effect on a body at L2.
The L3 point lies on the line defined by the two large masses, beyond the larger of the two.
The L4 and L5 points lie at the third corners of the two equilateral triangles in the plane of orbit whose common base is the line between the centers of the two masses, such that the point lies behind (L5) or ahead (L4) of the smaller mass with regard to its orbit around the larger mass.
The triangular points (L4 and L5) are stable equilibria, provided that the ratio of M1/M2 is greater than 24.96. This is the case for the Sun–Earth system, the Sun–Jupiter system, and, by a smaller margin, the Earth–Moon system. When a body at these points is perturbed, it moves away from the point, but the factor opposite of that which is increased or decreased by the perturbation (either gravity or angular momentum-induced speed) will also increase or decrease, bending the object's path into a stable, kidney-bean-shaped orbit around the point (as seen in the corotating frame of reference).
In contrast to L4 and L5, where stable equilibrium exists, the points L1, L2, and L3 are positions of unstable equilibrium. Any object orbiting at L1, L2, or L3 will tend to fall out of orbit; it is therefore rare to find natural objects there, and spacecraft inhabiting these areas must employ station keeping in order to maintain their position.
Natural objects at Lagrangian points
It is common to find objects at or orbiting the L4 and L5 points of natural orbital systems. These are commonly called "trojans"; in the 20th century, asteroids discovered orbiting at the Sun–Jupiter L4 and L5 points were named after characters from Homer's Iliad. Asteroids at the L4 point, which leads Jupiter, are referred to as the "Greek camp", whereas those at the L5 point are referred to as the "Trojan camp". See also Trojan (astronomy).
Other examples of natural objects orbiting at Lagrange points:
Mathematical details
Lagrangian points are the constant-pattern solutions of the restricted three-body problem. For example, given two massive bodies in orbits around their common barycenter, there are five positions in space where a third body, of comparatively negligible mass, could be placed so as to maintain its position relative to the two massive bodies. As seen in a rotating reference frame that matches the angular velocity of the two co-orbiting bodies, the gravitational fields of two massive bodies combined with the minor body's centrifugal force are in balance at the Lagrangian points, allowing the smaller third body to be relatively stationary with respect to the first two.
L1
The location of L1 is the solution to the following equation, balancing gravitation and the centrifugal force:
where r is the distance of the L1 point from the smaller object, R is the distance between the two main objects, and M1 and M2 are the masses of the large and small object, respectively. (The quantity in parentheses on the right is the distance of L1 from the center of mass.) Solving this for r involves solving a quintic function, but if the mass of the smaller object (M2) is much smaller than the mass of the larger object (M1) then L1 and L2 are at approximately equal distances r from the smaller object, equal to the radius of the Hill sphere, given by:
This distance can be described as being such that the orbital period, corresponding to a circular orbit with this distance as radius around M2 in the absence of M1, is that of M2 around M1, divided by √3 ≈ 1.73:
L2
The location of L2 is the solution to the following equation, balancing gravitation and inertia:
with parameters defined as for the L1 case. Again, if the mass of the smaller object (M2) is much smaller than the mass of the larger object (M1) then L2 is at approximately the radius of the Hill sphere, given by:
L3
The location of L3 is the solution to the following equation, balancing gravitation and the centrifugal force:
with parameters defined as for the L1 and L2 cases except that r now indicates how much closer L3 is to the more massive object than the smaller object. If the mass of the smaller object (M2) is much smaller than the mass of the larger object (M1) then:
L4 and L5
The reason these points are in balance is that, at L4 and L5, the distances to the two masses are equal. Accordingly, the gravitational forces from the two massive bodies are in the same ratio as the masses of the two bodies, and so the resultant force acts through the barycenter of the system; additionally, the geometry of the triangle ensures that the resultant acceleration is to the distance from the barycenter in the same ratio as for the two massive bodies. The barycenter being both the center of mass and center of rotation of the three-body system, this resultant force is exactly that required to keep the smaller body at the Lagrange point in orbital equilibrium with the other two larger bodies of system. (Indeed, the third body need not have negligible mass.) The general triangular configuration was discovered by Lagrange in work on the three-body problem.
Stability
Although the L1, L2, and L3 points are nominally unstable, it turns out that it is possible to find (unstable) periodic orbits around these points, at least in the restricted three-body problem. These periodic orbits, referred to as "halo" orbits, do not exist in a full n-body dynamical system such as the Solar System. However, quasi-periodic (i.e. bounded but not precisely repeating) orbits following Lissajous-curve trajectories do exist in the n-body system. These quasi-periodic Lissajous orbits are what most of Lagrangian-point missions to date have used. Although they are not perfectly stable, a relatively modest effort at station keeping can allow a spacecraft to stay in a desired Lissajous orbit for an extended period of time. It also turns out that, at least in the case of Sun–Earth-L1 missions, it is actually preferable to place the spacecraft in a large-amplitude (100,000–200,000 km or 62,000–124,000 mi) Lissajous orbit, instead of having it sit at the Lagrangian point, because this keeps the spacecraft off the direct line between Sun and Earth, thereby reducing the impact of solar interference on Earth–spacecraft communications. Similarly, a large-amplitude Lissajous orbit around L2 can keep a probe out of Earth's shadow and therefore ensures a better illumination of its solar panels.
Sun–Earth
Sun–Earth L1 is suited for making observations of the Sun–Earth system. Objects here are never shadowed by Earth or the Moon. The first mission of this type was the International Sun Earth Explorer 3 (ISEE-3) mission used as an interplanetary early warning storm monitor for solar disturbances. Since June 2015, DSCOVR has orbited the L1 point.
Sun–Earth L2 is a good spot for space-based observatories. Because an object around L2 will maintain the same relative position with respect to the Sun and Earth, shielding and calibration are much simpler. It is, however, slightly beyond the reach of Earth's umbra, so solar radiation is not completely blocked. From this point, the Sun, Earth and Moon are relatively closely positioned together in the sky, and hence leave a large field of view without interference – this is especially helpful for infrared astronomy.
Sun–Earth L3 was a popular place to put a "Counter-Earth" in pulp science fiction and comic books. Once space-based observation became possible via satellites and probes, it was shown to hold no such object. The Sun–Earth L3 is unstable and could not contain a natural object, large or small, for very long. This is because the gravitational forces of the other planets are stronger than that of Earth (Venus, for example, comes within 0.3 AU of this L3 every 20 months).
A spacecraft orbiting near Sun–Earth L3 would be able to closely monitor the evolution of active sunspot regions before they rotate into a geoeffective position, so that a 7-day early warning could be issued by the NOAA Space Weather Prediction Center. Moreover, a satellite near Sun–Earth L3 would provide very important observations not only for Earth forecasts, but also for deep space support (Mars predictions and for manned mission to near-Earth asteroids). In 2010, spacecraft transfer trajectories to Sun–Earth L3 were studied and several designs were considered.
Missions to Lagrangian points generally orbit the points rather than occupy them directly.
Another interesting and useful property of the collinear Lagrangian points and their associated Lissajous orbits is that they serve as "gateways" to control the chaotic trajectories of the Interplanetary Transport Network.
Earth–Moon
Earth–Moon L1 allows comparatively easy access to Lunar and Earth orbits with minimal change in velocity and this has as an advantage to position a half-way manned space station intended to help transport cargo and personnel to the Moon and back.
Earth–Moon L2 would be a good location for a communications satellite covering the Moon's far side and would be "an ideal location" for a propellant depot as part of the proposed depot-based space transportation architecture.
Sun–Venus
Scientists at the B612 Foundation are planning to use Venus's L3 point to position their planned Sentinel telescope, which aims to look back towards Earth's orbit and compile a catalogue of near-Earth asteroids.
Spacecraft at Sun–Earth L1
International Sun Earth Explorer 3 (ISEE-3) began its mission at the Sun–Earth L1 before leaving to intercept a comet in 1982. The Sun–Earth L1 is also the point to which the Reboot ISEE-3 mission was attempting to return the craft as the first phase of a recovery mission (as of September 25, 2014 all efforts have failed and contact was lost).
Solar and Heliospheric Observatory (SOHO) is stationed in a halo orbit at L1, and the Advanced Composition Explorer (ACE) in a Lissajous orbit. WIND is also at L1.
Deep Space Climate Observatory (DSCOVR), launched on 11 February 2015, began orbiting L1 on 8 June 2015 to study the solar wind and its effects on Earth. DSCOVR is unofficially known as GORESAT, because it carries a camera always oriented to Earth and capturing full-frame photos of the planet similar to the Blue Marble. This concept was proposed by then-Vice President of the United States Al Gore in 1998 and was a centerpiece in his film An Inconvenient Truth.
LISA Pathfinder (LPF) was launched on 3 December 2015, and arrived at L1 on 22 January 2016, where, among other experiments, it will test the technology needed by (e)LISA to detect gravitational waves. LISA Pathfinder uses an instrument consisting of two small gold alloy cubes.
Spacecraft at Sun–Earth L2
Spacecraft at the Sun–Earth L2 point are in a Lissajous orbit until decommissioned, when they are sent into a heliocentric graveyard orbit.
