Kuramoto model - Alchetron, The Free Social Encyclopedia

The Kuramoto model, first proposed by Yoshiki Kuramoto (蔵本由紀 Kuramoto Yoshiki) , is a mathematical model used to describe synchronization. More specifically, it is a model for the behavior of a large set of coupled oscillators . Its formulation was motivated by the behavior of systems of chemical and biological oscillators, and it has found widespread applications such as in neuroscience . and oscillating flame dynamics. Kuramoto was quite surprised when the behavior of some physical systems, namely coupled arrays of Josephson junctions followed his model.

Definition

In the most popular version of the Kuramoto model, each of the oscillators is considered to have its own intrinsic natural frequency ω i , and each is coupled equally to all other oscillators. Surprisingly, this fully nonlinear model can be solved exactly, in the infinite-N limit, with a clever transformation and the application of self-consistency arguments.

The most popular form of the model has the following governing equations:

d θ i d t = ω i + K N ∑ j = 1 N sin ⁡ ( θ j − θ i ) , i = 1 … N ,

where the system is composed of N limit-cycle oscillators, with phases θ i and coupling K.

Noise can be added to the system. In that case, the original equation is altered to:

d θ i d t = ω i + ζ i + K N ∑ j = 1 N sin ⁡ ( θ j − θ i ) ,

where ζ i is the fluctuation and a function of time. If we consider the noise to be white noise, then

⟨ ζ i ( t ) ⟩ = 0 , ⟨ ζ i ( t ) ζ j ( t ′ ) ⟩ = 2 D δ i j δ ( t − t ′ )

with D denoting the strength of noise.

Transformation

The transformation that allows this model to be solved exactly (at least in the N → ∞ limit) is as follows. Define the "order" parameters r and ψ as

r e i ψ = 1 N ∑ j = 1 N e i θ j .

Here r represents the phase-coherence of the population of oscillators, and ψ indicates the average phase. Multiplying this equation with e − i θ i and then only considering the imaginary part gives

d θ i d t = ω i + K r sin ⁡ ( ψ − θ i ) .

Thus the oscillators' equations are no longer explicitly coupled; instead the order parameters govern the behavior. A further transformation is usually done, to a rotating frame in which the statistical average of phases over all oscillators is zero. That is, ψ = 0 . Finally, the governing equation becomes

d θ i d t = ω i − K r sin ⁡ ( θ i ) .

Large N limit

Now consider the case as N tends to infinity. Take the distribution of intrinsic natural frequencies as g(ω) (assumed normalized). Then assume that the density of oscillators at a given phase θ, with given natural frequency ω, at time t is ρ ( θ , ω , t ) . Normalization requires that

∫ − π π ρ ( θ , ω , t ) d θ = 1.

The continuity equation for oscillator density will be

∂ ρ ∂ t + ∂ ∂ θ [ ρ v ] = 0 ,

where v is the drift velocity of the oscillators given by taking the infinite-N limit in the transformed governing equation, i.e.,

∂ ρ ∂ t + ∂ ∂ θ [ ρ ω + ρ K r sin ⁡ ( ψ − θ ) ] = 0.

Finally, we must rewrite the definition of the order parameters for the continuum (infinite N) limit. θ i must be replaced by its ensemble average (over all ω) and the sum must be replaced by an integral, to give

r e i ψ = ∫ − π π e i θ ∫ − ∞ ∞ ρ ( θ , ω , t ) g ( ω ) d ω d θ .

Solutions

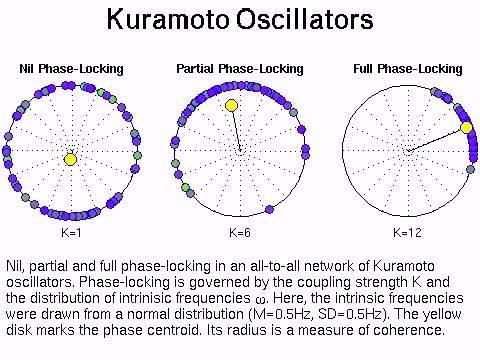
The incoherent state with all oscillators drifting randomly corresponds to the solution ρ = 1 / ( 2 π ) . In that case r = 0 , and there is no coherence among the oscillators. They are uniformly distributed across all possible phases, and the population is in a statistical steady-state (although individual oscillators continue to change phase in accordance with their intrinsic ω).

When coupling K is sufficiently strong, a fully synchronized solution is possible. In the fully synchronized state, all the oscillators share a common frequency, although their phases can be different.

A solution for the case of partial synchronization yields a state in which only some oscillators (those near the ensemble's mean natural frequency) synchronize; other oscillators drift incoherently. Mathematically, the state has

ρ = δ ( θ − ψ − arcsin ⁡ ( ω K r ) )

for locked oscillators, and

ρ = n o r m a l i z a t i o n c o n s t a n t ( ω − K r sin ⁡ ( θ − ψ ) )

for drifting oscillators. The cutoff occurs when | ω | < K r .

Connection to Hamiltonian Systems

The dissipative Kuramoto model is contained in certain conservative Hamiltonian systems with Hamiltonian of the form

H ( q 1 , … , q N , p 1 , … , p N ) = ∑ i = 1 N ω i 2 ( q i 2 + p i 2 ) + K 4 N ∑ i , j = 1 N ( q i p j − q j p i ) ( q j 2 + p j 2 − q i 2 − p i 2 )

After a canonical transformation to action-angle variables with actions I i = ( q i 2 + p i 2 ) / 2 and angles (phases) ϕ i = a r c t a n 2 ( q i / p i ) , exact Kuramoto dynamics emerges on invariant manifolds of constant I i ≡ I . With the transformed Hamiltonian

H ′ ( I 1 , … I N , θ 1 … , θ N ) = ∑ i = 1 N ω i I i − K N ∑ i = 1 N ∑ j = 1 N I j I i ( I j − I i ) sin ⁡ ( ϕ j − ϕ i ) ,

Hamilton's equation of motion become

d I i d t = − ∂ H ′ ∂ ϕ i = − 2 K N ∑ k = 1 N I k I i ( I k − I i ) cos ⁡ ( ϕ k − ϕ i )

and

d ϕ i d t = ∂ H ′ ∂ I i = ω i + K N ∑ k = 1 N [ 2 I i I k sin ⁡ ( ϕ k − ϕ i ) + I k / I i ( I k − I i ) sin ⁡ ( ϕ k − ϕ i ) ] .

So the manifold with I j = I is invariant because d I i d t = 0 and the phase dynamics d ϕ i d t becomes the dynamics of the Kuramoto model (with the same coupling constants for I = 1 / 2 ). The class of Hamiltonian systems characterizes certain quantum-classical systems including Bose-Einstein condensates.

Variations on the models

There are two types of variations of models based on the original model presented above, one that deals with changing the topological structure of the model; the second are more related to models that are inspired by Kuramoto model but don't have the same functional form.

Variations on topology

Beside the original model, which has an all-to-all topology, a sufficiently dense complex network-like topology is amenable to the mean-field treatment used in the solution of the original model (see Transformation and Large N Limit above for more info). One also may ask for the behavior of models in which there are intrinsically local, like one-dimensional topologies which the chain and the ring are prototypical examples. In such topologies, in which the coupling is not scalable according to 1/N, it's not possible to apply the canonical mean-field approach, so one must relies upon case-by-case analysis, making use of symmetries whenever it is possible, which may give basis for abstraction of general principles of solutions.

Uniform synchrony, waves and spirals can readily be observed in two-dimensional Kuramoto networks with diffusive local coupling. The stability of waves in these models can be determined analytically using the methods of Turing stability analysis. Uniform synchrony tends to be stable when the local coupling is everywhere positive whereas waves arise when the long-range connections are negative (inhibitory surround coupling). Waves and synchrony are connected by a topologically distinct branch of solutions known as ripple. These are low-amplitude spatially-periodic deviations that emerge from the uniform state (or the wave state) via a Hopf birfurcation. The existence of ripple solutions was predicted by Wiley, Strogatz and Girvan who called them multi-twisted q-states.

Variations on the phase interaction

Kuramoto approximated the phase interaction between any two oscillators by its first Fourier component, namely Γ ( ϕ ) = sin ⁡ ( ϕ ) , where ϕ = θ j − θ i . Better approximations can be obtained by including higher-order Fourier components,

Γ ( ϕ ) = sin ⁡ ( ϕ ) + a 1 sin ⁡ ( 2 ϕ + b 1 ) + . . . + a n sin ⁡ ( 2 n ϕ + b n ) ,

where parameters a i and b i must be estimated. For example, synchronization among a network of weakly-coupled Hodgkin-Huxley neurons can be replicated using coupled oscillators that retain the first four Fourier components of the interaction function . The introduction of higher-order phase interaction terms can also induce interesting synchronization phenomena such as heteroclinic cycles and Chimeras.

References

Kuramoto model Wikipedia

(Text) CC BY-SA

Contents