Katz centrality

Measuring Katz centrality

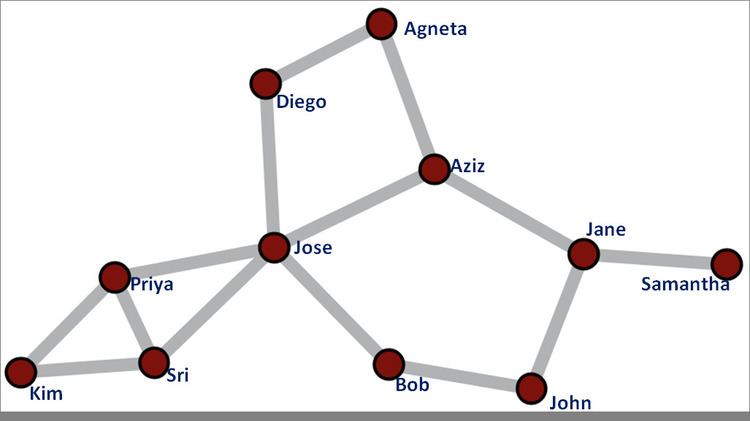
Katz centrality computes the relative influence of a node within a network by measuring the number of the immediate neighbors (first degree nodes) and also all other nodes in the network that connect to the node under consideration through these immediate neighbors. Connections made with distant neighbors are, however, penalized by an attenuation factor α . Each path or connection between a pair of nodes is assigned a weight determined by α and the distance between nodes as α d .

For example, in the figure on the right, assume that John’s centrality is being measured and that α = 0.5 . The weight assigned to each link that connects John with his immediate neighbors Jane and Bob will be ( 0.5 ) 1 = 0.5 . Since Jose connects to John indirectly through Bob, the weight assigned to this connection (composed of two links) will be ( 0.5 ) 2 = 0.25 . Similarly, the weight assigned to the connection between Agneta and John through Aziz and Jane will be ( 0.5 ) 3 = 0.125 and the weight assigned to the connection between Agneta and John through Diego, Jose and Bob will be ( 0.5 ) 4 = 0.0625 .

Mathematical formulation

Let A be the adjacency matrix of a network under consideration. Elements ( a i j ) of A are variables that take a value 1 if a node i is connected to node j and 0 otherwise. The powers of A indicate the presence (or absence) of links between two nodes through intermediaries. For instance, in matrix A 3 , if element ( a 2 , 12 ) = 1 , it indicates that node 2 and node 12 are connected through some first and second degree neighbors of node 2. If C K a t z ( i ) denotes Katz centrality of a node i, then mathematically:

Note that the above definition uses the fact that the element at location ( i , j ) of the adjacency matrix A raised to the power k (i.e. A k ) reflects the total number of k degree connections between nodes i and j . The value of the attenuation factor α has to be chosen such that it is smaller than the reciprocal of the absolute value of the largest eigenvalue of the adjacency matrix A. In this case the following expression can be used to calculate Katz centrality:

Here I is the identity matrix, I → is an identity vector of size n (n is the number of nodes) consisting of ones. A T denotes the transposed matrix of A and ( I − α A T ) − 1 denotes matrix inversion of the term ( I − α A T ) .

Applications

Katz centrality can be used to compute centrality in directed networks such as citation networks and the World Wide Web. Katz centrality is more suitable in the analysis of directed acyclic graphs where traditionally used measures like eigenvector centrality are rendered useless. Katz centrality can also be used in estimating the relative status or influence of actors in a social network. In neuroscience, it is found that Katz centrality correlates with the relative firing rate of neurons in a neural network.