 | ||
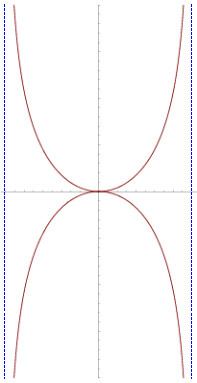
In geometry, the kappa curve or Gutschoven's curve is a two-dimensional algebraic curve resembling the Greek letter ϰ (kappa). The kappa curve was first studied by Gérard van Gutschoven around 1662. In the history of mathematics, it is remembered as one of the first examples of Isaac Barrow's application of rudimentary calculus methods to determine the tangent of a curve. Isaac Newton and Johann Bernoulli continued the studies of this curve subsequently.
Contents
Using the Cartesian coordinate system it can be expressed as
or, using parametric equations,
In polar coordinates its equation is even simpler:
It has two vertical asymptotes at
The kappa curve's curvature:
Tangential angle:
Tangents via infinitesimals
The tangent lines of the kappa curve can also be determined geometrically using differentials and the elementary rules of infinitesimal arithmetic. Suppose x and y are variables, while a is taken as a constant. From the definition of the kappa curve,
Now, an infinitesimal change in our location must also change the value of the left hand side, so
Distributing the differential and applying appropriate rules,
Derivative
If we use the modern concept of a functional relationship y(x) and apply implicit differentiation, the slope of a tangent line to the kappa curve at a point (x,y) is :
