 | ||
The k rm n line by michael rywalt footage from the us space shuttle program
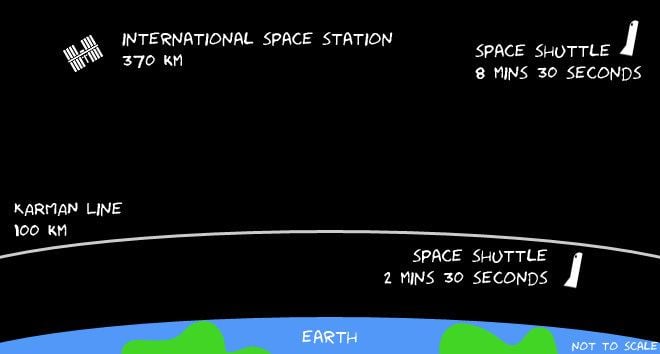
The Kármán line, or Karman line, lies at an altitude of 100 kilometres (62 mi; 330,000 ft) above the Earth's sea level, and commonly represents the boundary between the Earth's atmosphere and outer space. This definition is accepted by the Fédération Aéronautique Internationale (FAI), which is an international standard-setting and record-keeping body for aeronautics and astronautics.
Contents
- The k rm n line by michael rywalt footage from the us space shuttle program
- Krmns comments
- Definition
- Interpretations of the definition
- Alternatives to the definition
- References

The line is named after Theodore von Kármán (1881–1963), a Hungarian-American engineer and physicist. He was active primarily in aeronautics and astronautics. He was the first to calculate that around this altitude, the atmosphere becomes too thin to support aeronautical flight, because a vehicle at this altitude would have to travel faster than orbital velocity to derive sufficient aerodynamic lift to support itself. The line is approximately at the turbopause, above which atmospheric gasses are not well-mixed. The mesopause atmospheric temperature minimum has been measured variously at 85 km or 100 km, which puts the line at or near the bottom of the thermosphere.

Kármán's comments
In the final chapter of his autobiography Kármán addresses the issue of the edge of outer space:
Definition

An atmosphere does not abruptly end at any given height, but becomes progressively thinner with altitude. Also, depending on how the various layers that make up the space around the Earth are defined (and depending on whether these layers are considered part of the actual atmosphere), the definition of the edge of space could vary considerably: If one were to consider the thermosphere and exosphere part of the atmosphere and not of space, one might have to extend the boundary to space to at least 10,000 km (6,200 mi) above sea level. The Kármán line thus is an arbitrary definition based on the following considerations:

An aircraft only stays aloft if it constantly travels forward relative to the air (airspeed is not dependent on speed relative to ground), so that the wings can generate lift. The thinner the air, the faster the plane must go to generate enough lift to stay up.
The amount of lift required at any given point can be calculated by the lift equation:
where
L is the lift forceρ is the air densityv is the aircraft's speed relative to the airS is the aircraft's wing area,CL is the lift coefficient.
Lift (L) generated is directly proportional to the air density (ρ). All other factors remaining unchanged, true airspeed (v) must increase to compensate for less air density (ρ) at higher altitudes.
An orbiting spacecraft only stays in the sky if the centrifugal component of its movement around the Earth is enough to balance the downward pull of gravity. If it goes slower, the pull of gravity gradually makes its altitude decrease. The required speed is called orbital velocity, and it varies with the height of the orbit. For the International Space Station, or a space shuttle in low Earth orbit, the orbital velocity is about 27,000 km per hour (17,000 miles per hour).
For an airplane flying higher and higher, the increasingly thin air provides less and less lift, requiring increasingly higher speed to create enough lift to hold the airplane up. It eventually reaches an altitude where it must fly so fast to generate lift that it reaches orbital velocity. The Kármán line is the altitude where the speed necessary to aerodynamically support the airplane's full weight equals orbital velocity (assuming wing loading of a typical airplane). In practice, supporting full weight wouldn't be necessary to maintain altitude because the curvature of the Earth adds centrifugal lift as the airplane reaches orbital speed. However, the Karman line definition ignores this effect because orbital velocity is implicitly sufficient to maintain any altitude regardless of atmospheric density. The Karman line is therefore the highest altitude at which orbital speed provides sufficient aerodynamic lift to fly in a straight line that doesn't follow the curvature of the Earth's surface.
Above 100 kilometers the air density is about 1/2200000 the density on the surface. At the Karman line, the air density ρ is such that
where
v0 is the speed of a circular orbit at the same altitude in vacuumm is the mass of the aircraftg is the acceleration due to gravity.Although the calculated altitude was not exactly 100 km, Kármán proposed that 100 km be the designated boundary to space, because the round number is more memorable, and the calculated altitude varies minutely as certain parameters are varied. An international committee recommended the 100 km line to the FAI, and upon adoption, it became widely accepted as the boundary to space for many purposes. However, there is still no international legal definition of the demarcation between a country's air space and outer space.
Another hurdle to strictly defining the boundary to space is the dynamic nature of Earth's atmosphere. For example, at an altitude of 1,000 km (620 mi), the atmosphere's density can vary by a factor of five, depending on the time of day, time of year, AP magnetic index, and recent solar flux.
The FAI uses the Kármán line to define the boundary between aeronautics and astronautics:
Interpretations of the definition
Some people (including the FAI in some of their publications) also use the expression "edge of space" to refer to a region below the conventional 100 km boundary to space, which is often meant to include substantially lower regions as well. Thus, certain balloon or airplane flights might be described as "reaching the edge of space". In such statements, "reaching the edge of space" merely refers to going higher than average aeronautical vehicles commonly would.
In 1963 Andrew G. Haley discussed the Kármán line in his book Space Law and Government. In a chapter on the limits of national sovereignty, he made a survey of major writers’ views. He indicated the inherent imprecision of the Line:
The line represents a mean or median measurement. It is comparable to such measures used in the law as mean sea level, meander line, tide line; but it is more complex than these. In arriving at the von Kármán jurisdictional line, myriad factors must be considered – other than the factor of aerodynamic lift. These factors have been discussed in a very large body of literature and by a score or more of commentators. They include the physical constitution of the air; the biological and physiological viability; and still other factors which logically join to establish a point at which air no longer exists and at which airspace ends.Alternatives to the definition
The U.S. Air Force definition of an astronaut is a person who has flown more than 50 miles (~80 km) above mean sea level, approximately the line between the mesosphere and the thermosphere. NASA uses the FAI's 100-kilometer figure. The United States does not officially define a boundary of space. In 2005, three veteran NASA X-15 pilots (John B. McKay, William H. Dana and Joseph Albert Walker) were retroactively (two posthumously) awarded their astronaut wings, as they had flown between 90 km (56 mi) and 108 km (67 mi) in the 1960s, but at the time had not been recognized as astronauts. The latter altitude exceeds the modern international definition of the boundary of space.
Another definition proposed in international law discussions defines the lower boundary of space as the lowest perigee attainable by an orbiting space vehicle, but does not specify an altitude. Due to atmospheric drag, the lowest altitude at which an object in a circular orbit can complete at least one full revolution without propulsion is approximately 150 km (90 mi), whereas an object can maintain an elliptical orbit with perigee as low as about 130 km (80 mi) with propulsion. Above altitudes of approximately 160 km (100 mi) the sky is completely black.
