Joule–Thomson effect

History

The effect is named after James Prescott Joule and William Thomson, 1st Baron Kelvin, who discovered it in 1852. It followed upon earlier work by Joule on Joule expansion, in which a gas undergoes free expansion in a vacuum and the temperature is unchanged, if the gas is ideal.

Description

The adiabatic (no heat exchanged) expansion of a gas may be carried out in a number of ways. The change in temperature experienced by the gas during expansion depends not only on the initial and final pressure, but also on the manner in which the expansion is carried out.

If the expansion process is reversible, meaning that the gas is in thermodynamic equilibrium at all times, it is called an isentropic expansion. In this scenario, the gas does positive work during the expansion, and its temperature decreases.

In a free expansion, on the other hand, the gas does no work and absorbs no heat, so the internal energy is conserved. Expanded in this manner, the temperature of an ideal gas would remain constant, but the temperature of a real gas decreases, except at very high temperature.

The method of expansion discussed in this article, in which a gas or liquid at pressure P₁ flows into a region of lower pressure P₂ without significant change in kinetic energy, is called the Joule–Thomson expansion. The expansion is inherently irreversible. During this expansion, enthalpy remains unchanged (see proof below). Unlike a free expansion, work is done, causing a change in internal energy. Whether the internal energy increases or decreases is determined by whether work is done on or by the fluid; that is determined by the initial and final states of the expansion and the properties of the fluid.

The temperature change produced during a Joule–Thomson expansion is quantified by the Joule–Thomson coefficient, μ J T . This coefficient may be either positive (corresponding to cooling) or negative (heating); the regions where each occurs for molecular nitrogen, N₂, are shown in the figure. Note that most conditions in the figure correspond to N₂ being a supercritical fluid, where it has some properties of a gas and some of a liquid, but can not be really described as being either. The coefficient is negative at both very high and very low temperatures; at very high pressure it is negative at all temperatures. The maximum inversion temperature (621 K for N₂) occurs as zero pressure is approached. For N₂ gas at low pressures, μ J T is negative at high temperatures and positive at low temperatures. At temperatures below the gas-liquid coexistence curve, N₂ condenses to form a liquid and the coefficient again becomes negative. Thus, for N₂ gas below 621 K, a Joule–Thomson expansion can be used to cool the gas until liquid N₂ forms.

Physical mechanism

There are two factors that can change the temperature of a fluid during an adiabatic expansion: a change in internal energy or the conversion between potential and kinetic internal energy. Temperature is the measure of thermal kinetic energy (energy associated with molecular motion); so a change in temperature indicates a change in thermal kinetic energy. The internal energy is the sum of thermal kinetic energy and thermal potential energy. Thus, even if the internal energy does not change, the temperature can change due to conversion between kinetic and potential energy; this is what happens in a free expansion and typically produces a decrease in temperature as the fluid expands. If work is done on or by the fluid as it expands, then the total internal energy changes. This is what happens in a Joule–Thomson expansion and can produce larger heating or cooling than observed in a free expansion.

In a Joule–Thomson expansion the enthalpy remains constant. The enthalpy, H , is defined as

H = U + P V

where U is internal energy, P is pressure, and V is volume. Under the conditions of a Joule–Thomson expansion, the change in P V represents the work done by the fluid (see the proof below). If P V increases, with H constant, then U must decrease as a result of the fluid doing work on its surroundings. This produces a decrease in temperature and results in a positive Joule–Thomson coefficient. Conversely, a decrease in P V means that work is done on the fluid and the internal energy increases. If the increase in internal energy exceeds the increase in potential energy, there will be an increase in the temperature of the fluid and the Joule–Thomson coefficient will be negative.

For an ideal gas, P V does not change during a Joule–Thomson expansion. As a result, there is no change in internal energy; since there is also no change in thermal potential energy, there can be no change in thermal kinetic energy and, therefore, no change in temperature. In real gases, P V does change.

The ratio of the value of P V to that expected for an ideal gas at the same temperature is called the compressibility factor, Z . For a gas, this is typically less than unity at low temperature and greater than unity at high temperature (see the discussion in compressibility factor). At low pressure, the value of Z always moves towards unity as a gas expands. Thus at low temperature, Z and P V will increase as the gas expands, resulting in a positive Joule–Thomson coefficient. At high temperature, Z and P V decrease as the gas expands; if the decrease is large enough, the Joule–Thomson coefficient will be negative.

For liquids, and for supercritical fluids under high pressure, P V increases as pressure increases. This is due to molecules being forced together, so that the volume can barely decrease due to higher pressure. Under such conditions, the Joule–Thomson coefficient is negative, as seen in the figure above.

The physical mechanism associated with the Joule–Thomson effect is closely related to that of a shock wave, although a shock wave differs in that the change in bulk kinetic energy of the gas flow is not negligible.

The Joule–Thomson (Kelvin) coefficient

The rate of change of temperature T with respect to pressure P in a Joule–Thomson process (that is, at constant enthalpy H ) is the Joule–Thomson (Kelvin) coefficient μ J T . This coefficient can be expressed in terms of the gas's volume V , its heat capacity at constant pressure C p , and its coefficient of thermal expansion α as:

μ J T = ( ∂ T ∂ P ) H = V C p ( α T − 1 )

See the Derivation of the Joule–Thomson (Kelvin) coefficient below for the proof of this relation. The value of μ J T is typically expressed in °C/bar (SI units: K/Pa) and depends on the type of gas and on the temperature and pressure of the gas before expansion. Its pressure dependence is usually only a few percent for pressures up to 100 bar.

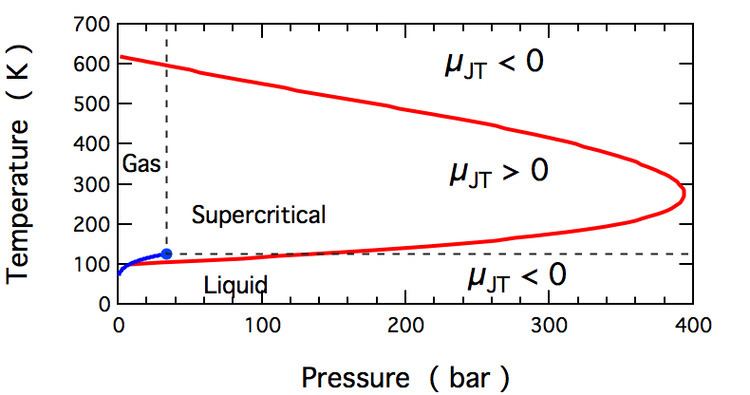
All real gases have an inversion point at which the value of μ J T changes sign. The temperature of this point, the Joule–Thomson inversion temperature, depends on the pressure of the gas before expansion.

In a gas expansion the pressure decreases, so the sign of ∂ P is negative by definition. With that in mind, the following table explains when the Joule–Thomson effect cools or warms a real gas:

Helium and hydrogen are two gases whose Joule–Thomson inversion temperatures at a pressure of one atmosphere are very low (e.g., about 45 K (−228 °C) for helium). Thus, helium and hydrogen warm when expanded at constant enthalpy at typical room temperatures. On the other hand, nitrogen and oxygen, the two most abundant gases in air, have inversion temperatures of 621 K (348 °C) and 764 K (491 °C) respectively: these gases can be cooled from room temperature by the Joule–Thomson effect.

For an ideal gas, μ J T is always equal to zero: ideal gases neither warm nor cool upon being expanded at constant enthalpy.

Applications

In practice, the Joule–Thomson effect is achieved by allowing the gas to expand through a throttling device (usually a valve) which must be very well insulated to prevent any heat transfer to or from the gas. No external work is extracted from the gas during the expansion (the gas must not be expanded through a turbine, for example).

The cooling produced in the Joule–Thomson expansion makes it a valuable tool in refrigeration. In vapor-compression refrigeration, as used in common refrigerators and air conditioners, it produces cooling in the throttling valve. The effect is applied in the Linde technique as a standard process in the petrochemical industry, where the cooling effect is used to liquefy gases, and also in many cryogenic applications (e.g. for the production of liquid oxygen, nitrogen, and argon). A gas must be below its inversion temperature to be liquefied by the Linde cycle. For this reason, simple Linde cycle liquefiers, starting from ambient temperature, cannot be used to liquefy helium, hydrogen, or neon. However, the Joule–Thomson effect can be used to liquefy even helium, provided that the helium gas is first cooled below its inversion temperature of 40 K.

Proof that the specific enthalpy remains constant

In thermodynamics so-called "specific" quantities are quantities per unit mass (kg) and are denoted by lower-case characters. So h, u, and v are the specific enthalpy, specific internal energy, and specific volume (volume per unit mass, or reciprocal density), respectively. In a Joule–Thomson process the specific enthalpy h remains constant. To prove this, the first step is to compute the net work done when a mass m of the gas moves through the plug. This amount of gas has a volume of V₁ = m v₁ in the region at pressure P₁ (region 1) and a volume V₂ = m v₂ when in the region at pressure P₂ (region 2). Then in region 1, the "flow work" done on the amount of gas by the rest of the gas is: W₁ = m P₁v₁. In region 2, the work done by the amount of gas on the rest of the gas is: W₂ = m P₂v₂. So, the total work done on the mass m of gas is

W = m P 1 v 1 − m P 2 v 2 .

The change in internal energy minus the total work done on the amount of gas is, by the first law of thermodynamics, the total heat supplied to the amount of gas.

U − W = Q

In the Joule–Thomson process the gas is insulated, so no heat is absorbed. This means that

( m u 2 − m u 1 ) − ( m P 1 v 1 − m P 2 v 2 ) = 0 m u 1 + m P 1 v 1 = m u 2 + m P 2 v 2 u 1 + P 1 v 1 = u 2 + P 2 v 2

where u₁ and u₂ denote the specific internal energies of the gas in regions 1 and 2, respectively. Using the definition of the specific enthalpy h = u + Pv, the above equation implies that

h 1 = h 2

where h₁ and h₂ denote the specific enthalpies of the amount of gas in regions 1 and 2, respectively.

Throttling in the T-s diagram

A very convenient way to get a quantitative understanding of the throttling process is by using diagrams. There are many types of diagrams (h-T diagram, h-P diagram, etc.) Commonly used are the so-called T-s diagrams. Figure 2 shows the T-s diagram of nitrogen as an example. Various points are indicated as follows:

a) T = 300 K, p = 200 bar, s = 5.16 kJ/(kgK), h = 430 kJ/kg;b) T = 270 K, p = 1 bar, s = 6.79 kJ/(kgK), h = 430 kJ/kg;c) T = 133 K, p = 200 bar, s = 3.75 kJ/(kgK), h = 150 kJ/kg;d) T = 77.2 K, p = 1 bar, s = 4.40 kJ/(kgK), h = 150 kJ/kg;e) T = 77.2 K, p = 1 bar, s = 2.83 kJ/(kgK), h = 28 kJ/kg (saturated liquid at 1 bar);f) T = 77.2 K, p = 1 bar, s = 5.41 kJ/(kgK), h =230 kJ/kg (saturated gas at 1 bar).

As shown before, throttling keeps h constant. E.g. throttling from 200 bar and 300 K (point a in fig. 2) follows the isenthalp (line of constant specific enthalpy) of 430 kJ/kg. At 1 bar it results in point b which has a temperature of 270 K. So throttling from 200 bar to 1 bar gives a cooling from room temperature to below the freezing point of water. Throttling from 200 bar and an initial temperature of 133 K (point c in fig. 2) to 1 bar results in point d, which is in the two-phase region of nitrogen at a temperature of 77.2 K. Since the enthalpy is an extensive parameter the enthalpy in d (h_d) is equal to the enthalpy in e (h_e) multiplied with the mass fraction of the liquid in d (x_d) plus the enthalpy in f (h_f) multiplied with the mass fraction of the gas in d (1 − x_d). So

h d = x d h e + ( 1 − x d ) h f .

With numbers: 150 = x_d 28 + (1 − x_d) 230 so x_d is about 0.40. This means that the mass fraction of the liquid in the liquid–gas mixture leaving the throttling valve is 40%.

Derivation of the Joule–Thomson coefficient

It is difficult to think physically about what the Joule–Thomson coefficient, μ J T , represents. Also, modern determinations of μ J T do not use the original method used by Joule and Thomson, but instead measure a different, closely related quantity. Thus, it is useful to derive relationships between μ J T and other, more convenient quantities. That is the purpose of this section.

The first step in obtaining these results is to note that the Joule–Thomson coefficient involves the three variables T, P, and H. A useful result is immediately obtained by applying the cyclic rule; in terms of these three variables that rule may be written

( ∂ T ∂ P ) H ( ∂ H ∂ T ) P ( ∂ P ∂ H ) T = − 1.

Each of the three partial derivatives in this expression has a specific meaning. The first is μ J T , the second is the constant pressure heat capacity, C p , defined by

C p = ( ∂ H ∂ T ) P

and the third is the inverse of the isothermal Joule–Thomson coefficient, μ T , defined by

μ T = ( ∂ H ∂ P ) T .

This last quantity is more easily measured than μ J T . Thus, the expression from the cyclic rule becomes

μ J T = − μ T C p .

This equation can be used to obtain Joule–Thomson coefficients from the more easily measured isothermal Joule–Thomson coefficient. It is used in the following to obtain a mathematical expression for the Joule–Thomson coefficient in terms of the volumetric properties of a fluid.

To proceed further, the starting point is the fundamental equation of thermodynamics in terms of enthalpy; this is

d H = T d S + V d P .

Now "dividing through" by dP, while holding temperature constant, yields

( ∂ H ∂ P ) T = T ( ∂ S ∂ P ) T + V

The partial derivative on the left is the isothermal Joule–Thomson coefficient, μ T , and the one on the right can be expressed in terms of the coefficient of thermal expansion via a Maxwell relation. The appropriate relation is

( ∂ S ∂ P ) T = − ( ∂ V ∂ T ) P = − V α

where α is the cubic coefficient of thermal expansion. Replacing these two partial derivatives yields

μ T = − T V α   + V .

This expression can now replace μ T in the earlier equation for μ J T to obtain

μ J T ≡ ( ∂ T ∂ P ) H = V C p ( α T − 1 ) .

This provides an expression for the Joule–Thomson coefficient in terms of the commonly available properties heat capacity, molar volume, and thermal expansion coefficient. It shows that the Joule–Thomson inversion temperature, at which μ J T is zero, occurs when the coefficient of thermal expansion is equal to the inverse of the temperature. Since this is true at all temperatures for ideal gases (see expansion in gases), the Joule–Thomson coefficient of an ideal gas is zero at all temperatures.

Joule's second law

It is easy to verify that for an ideal gas defined by suitable microscopic postulates that αT = 1, so the temperature change of such an ideal gas at a Joule–Thomson expansion is zero. For such an ideal gas, this theoretical result implies that:

The internal energy of a fixed mass of an ideal gas depends only on its temperature (not pressure or volume).

This rule was originally found by Joule experimentally for real gases and is known as Joule's second law. More refined experiments of course found important deviations from it.