Irrigation game

Mathematical definition

The definition of Márkus et al. 2011 is the following: A graph is a pair G = ( V ; A ) , where the elements of V are called vertices or nodes, and A stands for the ordered pairs of vertices, called arcs or edges. A rooted tree is a graph in which any two vertices are connected by exactly one simple path, and one vertex has been designated the root, in which case the edges have a natural orientation, away from the root. The tree-order is the partial ordering on the vertices of a rooted tree with i ≤ j , if the unique path from the root to j passes through i . For any e ∈ A , e = i j ¯ means e is an edge between vertices i ; j ∈ V such that i ≤ j .

Let c : A → R + . Then c and ( G ; c ) are called cost function and cost-tree respectively: for any e ∈ A , e = i j ¯ , c e is the cost of joining player j to player i .

Assume that the cost-tree problems have fixed, at least two, number of players ( # V ≥ 3 , # N ≥ 2 ). Let ( G ; c ) be a cost-tree, and N be the set of the players (the vertices but the root). Consider an S ⊆ N non-empty coalition, then the cost of connecting the players of S to the root is given by the cost of the minimal rooted tree which covers coalition S . By this method for each cost-tree we can define a game, called irrigation game. Formally:

Definition (Irrigation game): For any cost-tree ( G ; c ) , let N = V ∖ { r o o t } be the player set, and for any coalition S (the empty sum is 0) let

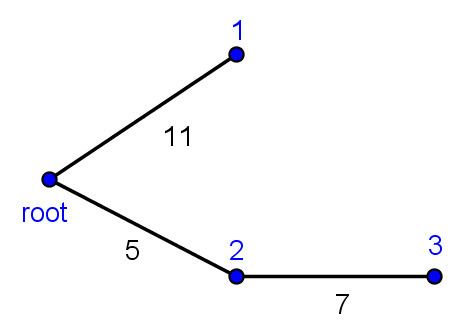
The above graph represents a simple irrigation game played by three players. G = ( V , A ) is as follows: V = { r o o t , 1 , 2 , 3 } , A = { r o o t 1 ¯ , r o o t 2 ¯ , 23 ¯ } , and the cost function c is defined as c ( r o o t 1 ¯ ) = 11 ,     c ( r o o t 2 ¯ ) = 5 and c ( 23 ¯ ) = 7 .

Then the irrigation game is the following: v ( G ; c ) ( ∅ ) = 0 , v ( G ; c ) ( { 1 } ) = 11 , v ( G ; c ) ( { 2 } ) = 5 , v ( G ; c ) ( { 3 } ) = 7 , v ( G ; c ) ( { 1 , 2 } ) = 16 , v ( G ; c ) ( { 1 , 3 } ) = 23 , v ( G ; c ) ( { 2 , 3 } ) = 12 , v ( G ; c ) ( { 1 , 2 , 3 } ) = 23.

Properties and Results

Márkus et al. 2011 reported several important properties of the class of the irrigation games. First, the well-known class of the airport games is a proper subset of the class of irrigation games, since the airport games are defined on special rooted trees, on chains (see: Airport problem). Second, the class of irrigation games is a non-convex cone which is a proper subset of the finite convex cone spanned by the duals of the unanimity games, therefore every irrigation game is concave.

Márkus et al. 2011 also extended the Shapley and Young axiomatizations of the Shapley value to the class of irrigation games and showed that the Shapley value of an irrigation game is always in the core of the game.