Rahul Sharma (Editor)

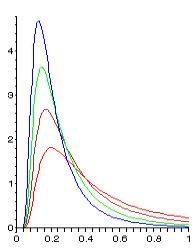
Inverse chi squared distribution

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Inverse-chi-squared distribution

Parameters
  
ν > 0 {\displaystyle \nu >0\!}

Support
  
x ∈ ( 0 , ∞ ) {\displaystyle x\in (0,\infty )\!}

PDF
  
2 − ν / 2 Γ ( ν / 2 ) x − ν / 2 − 1 e − 1 / ( 2 x ) {\displaystyle {\frac {2^{-\nu /2}}{\Gamma (\nu /2)}}\,x^{-\nu /2-1}e^{-1/(2x)}\!}

CDF
  
Γ ( ν 2 , 1 2 x ) / Γ ( ν 2 ) {\displaystyle \Gamma \!\left({\frac {\nu }{2}},{\frac {1}{2x}}\right){\bigg /}\,\Gamma \!\left({\frac {\nu }{2}}\right)\!}

Mean
  
1 ν − 2 {\displaystyle {\frac {1}{\nu -2}}\!} for ν > 2 {\displaystyle \nu >2\!}

Mode
  
1 ν + 2 {\displaystyle {\frac {1}{\nu +2}}\!}

In probability and statistics, the inverse-chi-squared distribution (or inverted-chi-square distribution) is a continuous probability distribution of a positive-valued random variable. It is closely related to the chi-squared distribution and its specific importance is that it arises in the application of Bayesian inference to the normal distribution, where it can be used as the prior and posterior distribution for an unknown variance.

Contents

Definition

The inverse-chi-squared distribution (or inverted-chi-square distribution ) is the probability distribution of a random variable whose multiplicative inverse (reciprocal) has a chi-squared distribution. It is also often defined as the distribution of a random variable whose reciprocal divided by its degrees of freedom is a chi-squared distribution. That is, if X has the chi-squared distribution with ν degrees of freedom, then according to the first definition, 1 / X has the inverse-chi-squared distribution with ν degrees of freedom; while according to the second definition, ν / X has the inverse-chi-squared distribution with ν degrees of freedom. Only the first definition will usually be covered in this article.

The first definition yields a probability density function given by

f 1 ( x ; ν ) = 2 − ν / 2 Γ ( ν / 2 ) x − ν / 2 − 1 e − 1 / ( 2 x ) ,

while the second definition yields the density function

f 2 ( x ; ν ) = ( ν / 2 ) ν / 2 Γ ( ν / 2 ) x − ν / 2 − 1 e − ν / ( 2 x ) .

In both cases, x > 0 and ν is the degrees of freedom parameter. Further, Γ is the gamma function. Both definitions are special cases of the scaled-inverse-chi-squared distribution. For the first definition the variance of the distribution is σ 2 = 1 / ν , while for the second definition σ 2 = 1 .


Differential equation

{ 2 x 2 f 1 ′ ( x ) + f 1 ( x ) ( ν x + 2 x − 1 ) = 0 , f 1 ( 1 ) = 2 − ν / 2 e Γ ( ν 2 ) }
{ 2 x 2 f 2 ′ ( x ) + f 2 ( x ) ( − ν + ν x + 2 x ) = 0 , f 2 ( 1 ) = ( 2 e ) − ν / 2 v ν / 2 Γ ( ν 2 ) }

  • chi-squared: If X ∼ χ 2 ( ν ) and Y = 1 X , then Y ∼ Inv- χ 2 ( ν )
  • scaled-inverse chi-squared: If X ∼ Scale-inv- χ 2 ( ν , 1 / ν ) , then X ∼ inv- χ 2 ( ν )
  • Inverse gamma with α = ν 2 and β = 1 2

    • References

    Inverse-chi-squared distribution Wikipedia
    (Text) CC BY-SA