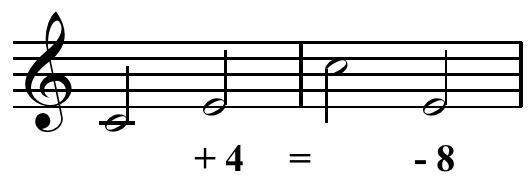 | ||
In musical set theory, an interval class (often abbreviated: ic), also known as unordered pitch-class interval, interval distance, undirected interval, or "(even completely incorrectly) as 'interval mod 6'" (Rahn 1980, 29; Whittall 2008, 273–74), is the shortest distance in pitch class space between two unordered pitch classes. For example, the interval class between pitch classes 4 and 9 is 5 because 9 − 4 = 5 is less than 4 − 9 = −5 ≡ 7 (mod 12). See modular arithmetic for more on modulo 12. The largest interval class is 6 since any greater interval n may be reduced to 12 − n.
Contents
Use of interval classes
The concept of interval class accounts for octave, enharmonic, and inversional equivalency. Consider, for instance, the following passage:
(To hear a MIDI realization, click the following: 106 KB
In the example above, all four labeled pitch-pairs, or dyads, share a common "intervallic color." In atonal theory, this similarity is denoted by interval class—ic 5, in this case. Tonal theory, however, classifies the four intervals differently: interval 1 as perfect fifth; 2, perfect twelfth; 3, diminished sixth; and 4, perfect fourth.
Notation of interval classes
The unordered pitch class interval i (a, b) may be defined as
where i <a, b> is an ordered pitch-class interval (Rahn 1980, 28).
While notating unordered intervals with parentheses, as in the example directly above, is perhaps the standard, some theorists, including Robert Morris (1991), prefer to use braces, as in i {a,b}. Both notations are considered acceptable.
