Interchangeability algorithm - Alchetron, the free social encyclopedia

In computer science, an interchangeability algorithm is a technique used to more efficiently solve constraint satisfaction problems (CSP). A CSP is a mathematical problem in which objects, represented by variables, are subject to constraints on the values of those variables; the goal in a CSP is to assign values to the variables that are consistent with the constraints. If two variables A and B in a CSP may be swapped for each other (that is, A is replaced by B and B is replaced by A) without changing the nature of the problem or its solutions, then A and B are interchangeable variables. Interchangeable variables represent a symmetry of the CSP and by exploiting that symmetry, the search space for solutions to a CSP problem may be reduced. For example, if solutions with A=1 and B=2 have been tried, then by interchange symmetry, solutions with B=1 and A=2 need not be investigated.

The concept of interchangeability and the interchangeability algorithm in constraint satisfaction problems was first introduced by Eugene Freuder in 1991. The interchangeability algorithm reduces the search space of backtracking search algorithms, thereby improving the efficiency of NP-Complete CSP problems.

Definitions

Fully Interchangeable

A value a for variable v is fully interchangeable with value b if and only if every solution in which v = a remains a solution when b is substituted for a and vice versa.

Neighbourhood Interchangeable

A value a for variable v is neighbourhood interchangeable with value b if and only if for every constraint on v, the values compatible with v = a are exactly those compatible with v = b.

Fully Substitutable

A value a for variable v is fully substitutable with value b if and only if every solution in which v = a remains a solution when b is substituted for a (but not necessarily vice versa).

Dynamically Interchangeable

A value a for variable v is dynamically interchangeable for b with respect to a set A of variable assignments if and only if they are fully interchangeable in the subproblem induced by A.

Neighborhood Interchangeability Algorithm

Finds neighborhood interchangeable values in a CSP. Repeat for each variable:

Build a discrimination tree by:Repeat for each value, v:

K-Interchangeability Algorithm

The algorithm can be used to explicitly find solutions to a constraint satisfaction problem. The algorithm can also be run for k steps as a preprocessor to simplify the subsequent backtrack search.

Finds k-interchangeable values in a CSP. Repeat for each variable:

Build a discrimination tree by:Repeat for each value, v:

Complexity Analysis

In the case of neighborhood interchangeable algorithm, if we assign the worst case bound to each loop. Then for n variables, which have at most d values for a variable, then we have a bound of : O ( n d ( n − l ) ∗ d ) = O ( n 2 d 2 ) .

Similarly, the complexity analysis of the k-interchangeability algorithm for a worst case O ( n k − 1 ) , with ( k − 1 ) -tuples of variables and d k − 1 , for ( k − 1 ) -tuples of values, then the bound is : O ( n d n k − l d k − 1 ) = O ( n k d k ) .

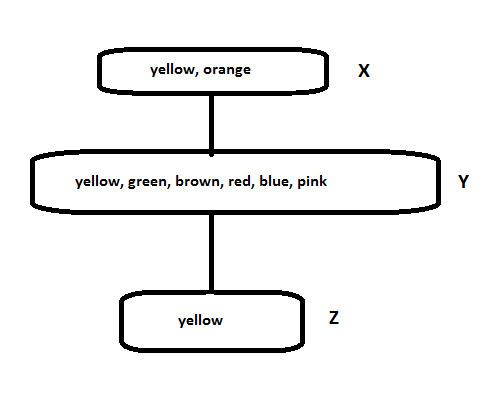
Example

The figure shows a simple graph coloring example with colors as vertices, such that no two vertices which are joined by an edge have the same color. The available colors at each vertex are shown. The colors yellow, green, brown, red, blue, pink represent vertex Y and are fully interchangeable by definition. For example, substituting maroon for green in the solution orange|X (orange for X), green|Y will yield another solution.

Applications

In Computer Science, the interchangeability algorithm has been extensively used in the fields of artificial intelligence, graph coloring problems, abstraction frame-works and solution adaptation.

References

Interchangeability algorithm Wikipedia

(Text) CC BY-SA

Contents