 | ||
In statistics, econometrics, epidemiology and related disciplines, the method of instrumental variables (IV) is used to estimate causal relationships when controlled experiments are not feasible or when a treatment is not successfully delivered to every unit in a randomized experiment. Intuitively, IV is used when the correlation between the explanatory variable and the dependent variable does not plausibly reflect the causal relationship between the two. A valid instrument induces changes in the explanatory variable but has no independent effect on the dependent variable, allowing a researcher to uncover the causal effect of the explanatory variable on the dependent variable.
Contents
- Introduction
- Example
- Selecting suitable instruments
- Estimation
- Interpretation as two stage least squares
- Non parametric analysis
- On the interpretation of IV estimates
- Potential problems
- Sampling properties and hypothesis testing
- Testing instrument strength and overidentifying restrictions
- References
Instrumental variable methods allow for consistent estimation when the explanatory variables (covariates) are correlated with the error terms in a regression model. Such correlation may occur when changes in the dependent variable change the value of at least one of the covariates ("reverse" causation), when there are omitted variables that affect both the dependent and independent variables, or when the covariates are subject to measurement error. Explanatory variables which suffer from one or more of these issues in the context of a regression are sometimes referred to as endogenous. In this situation, ordinary least squares produces biased and inconsistent estimates. However, if an instrument is available, consistent estimates may still be obtained. An instrument is a variable that does not itself belong in the explanatory equation but is correlated with the endogenous explanatory variables, conditional on the value of other covariates. In linear models, there are two main requirements for using IV:
Introduction
The concept of instrumental variables was first derived by Philip G. Wright, possibly in co-authorship with his son Sewall Wright, in the context of simultaneous equations in his 1928 book The Tariff on Animal and Vegetable Oils. In 1945, Olav Reiersøl applied the same approach in the context of errors-in-variables models in his dissertation, giving the method its name.
While the ideas behind IV extend to a broad class of models, a very common context for IV is in linear regression. Traditionally, an instrumental variable is defined as a variable Z that is correlated with the independent variable X and uncorrelated with the "error term" U in the linear equation
Note that
We can make this clearer by walking through the single-variable case. Suppose we are considering a regression with one variable and a constant (perhaps no other covariates are necessary, or perhaps we have partialed out any other relevant covariates):
In this case, the coefficient on the regressor of interest is given by
If
Of course, IV techniques have been developed among a much broader class of non-linear models. General definitions of instrumental variables, using counterfactual and graphical formalism, were given by Pearl (2000; p. 248). The graphical definition requires that Z satisfy the following conditions:
where
The counterfactual definition requires that Z satisfies
where Yx stands for the value that Y would attain had X been x and
If there are additional covariates W then the above definitions are modified so that Z qualifies as an instrument if the given criteria hold conditional on W.
The essence of Pearl's definition is:
- The equations of interest are "structural," not "regression."
- The error term U stands for all exogenous factors that affect Y when X is held constant.
- The instrument Z should be independent of U.
- The instrument Z should not affect Y when X is held constant (exclusion restriction).
- The instrument Z should not be independent of X.
These conditions do not rely on specific functional form of the equations and are applicable therefore to nonlinear equations, where U can be non-additive (see Non-parametric analysis). They are also applicable to a system of multiple equations, in which X (and other factors) affect Y through several intermediate variables. Note that an instrumental variable need not be a cause of X; a proxy of such cause may also be used, if it satisfies conditions 1-5. Note also that the exclusion restriction (condition 4) is redundant; it follows from conditions 2 and 3.
Example
Informally, in attempting to estimate the causal effect of some variable X on another Y, an instrument is a third variable Z which affects Y only through its effect on X. For example, suppose a researcher wishes to estimate the causal effect of smoking on general health. Correlation between health and smoking does not imply that smoking causes poor health because other variables may affect both health and smoking, or because health may affect smoking. It is at best difficult and expensive to conduct controlled experiments on smoking status in the general population. The researcher may attempt to estimate the causal effect of smoking on health from observational data by using the tax rate for tobacco products as an instrument for smoking. The tax rate for tobacco products is a reasonable choice for an instrument because the researcher assumes that it can only be correlated with health through its effect on smoking. If the researcher then finds tobacco taxes and state of health to be correlated, this may be viewed as evidence that smoking causes changes in health.
Angrist and Krueger (2001) present a survey of the history and uses of instrumental variable techniques.
Selecting suitable instruments
Since U is unobserved, the requirement that Z be independent of U cannot be inferred from data and must instead be determined from the model structure, i.e., the data-generating process. Causal graphs are a representation of this structure, and the graphical definition given above can be used to quickly determine whether a variable Z qualifies as an instrumental variable given a set of covariates W. To see how, consider the following example.
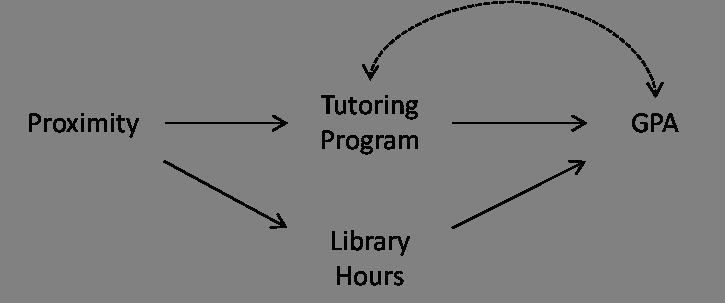
Suppose that we wish to estimate the effect of a university tutoring program on GPA. The relationship between attending the tutoring program and GPA may be confounded by a number of factors. Students that attend the tutoring program may care more about their grades or may be struggling with their work. This confounding is depicted in the Figures 1-3 on the right through the bidirected arc between Tutoring Program and GPA. If students are assigned to dormitories at random, the proximity of the student's dorm to the tutoring program is a natural candidate for being an instrumental variable.
However, what if the tutoring program is located in the college library? In that case, Proximity may also cause students to spend more time at the library, which in turn improves their GPA (see Figure 1). Using the causal graph depicted in the Figure 2, we see that Proximity does not qualify as an instrumental variable because it is connected to GPA through the path Proximity
Now, suppose that we notice that a student's "natural ability" affects his or her number of hours in the library as well as his or her GPA, as in Figure 3. Using the causal graph, we see that Library Hours is a collider and conditioning on it opens the path Proximity
Finally, suppose that Library Hours does not actually affect GPA because students who do not study in the library simply study elsewhere, as in Figure 4. In this case, controlling for Library Hours still opens a spurious path from Proximity to GPA. However, if we do not control for Library Hours and remove it as a covariate then Proximity can again be used an instrumental variable.
Estimation
We now revisit and expand upon the mechanics of IV in greater detail. Suppose the data are generated by a process of the form
where
The parameter
Suppose also that a regression model of nominally the same form is proposed. Given a random sample of T observations from this process, the ordinary least squares estimator is
where X, y and e denote column vectors of length T. Note the similarity of this equation to the equation involving
To recover the underlying parameter
Suppose that the relationship between each endogenous component x_i and the instruments is given by
The most common IV specification uses the following estimator:
Note that this specification approaches the true parameter as the sample gets large, so long as
As long as
Now an extension: suppose that there are more instruments than there are covariates in the equation of interest , so that Z is a T × M matrix with M > K. This is often called the over-identified case. In this case, the generalized method of moments (GMM) can be used. The GMM IV estimator is
where
Note that this expression collapses to the first when the number of instruments is equal to the number of covariates in the equation of interest. The over-identified IV is therefore a generalization of the just-identified IV.
Note that there is equivalent under-identified estimator for the case where m < k. Since the parameters are the solutions to a set of linear equations, an under-identified model using the set of equations
Interpretation as two-stage least squares
One computational method which can be used to calculate IV estimates is two-stage least squares (2SLS or TSLS). In the first stage, each explanatory variable that is an endogenous covariate in the equation of interest is regressed on all of the exogenous variables in the model, including both exogenous covariates in the equation of interest and the excluded instruments. The predicted values from these regressions are obtained.
Stage 1: Regress each column of X on Z, (
and save the predicted values:
In the second stage, the regression of interest is estimated as usual, except that in this stage each endogenous covariate is replaced with the predicted values from the first stage.
Stage 2: Regress Y on the predicted values from the first stage:
Which gives:
The resulting estimator of
Non-parametric analysis
When the form of the structural equations is unknown, an instrumental variable
where
Balke and Pearl [1997] derived tight bounds on ACE and showed that these can provide valuable information on the sign and size of ACE.
In linear analysis, there is no test to falsify the assumption the
On the interpretation of IV estimates
The exposition above assumes that the causal effect of interest does not vary across observations, that is, that
The standard IV estimator can recover local average treatment effects (LATE) rather than average treatment effects (ATE). Imbens and Angrist (1994) demonstrate that the linear IV estimate can be interpreted under weak conditions as a weighted average of local average treatment effects, where the weights depend on the elasticity of the endogenous regressor to changes in the instrumental variables. Roughly, that means that the effect of a variable is only revealed for the subpopulations affected by the observed changes in the instruments, and that subpopulations which respond most to changes in the instruments will have the largest effects on the magnitude of the IV estimate.
For example, if a researcher uses presence of a land-grant college as an instrument for college education in an earnings regression, she identifies the effect of college on earnings in the subpopulation which would obtain a college degree if a college is present but which would not obtain a degree if a college is not present. This empirical approach does not, without further assumptions, tell the researcher anything about the effect of college among people who would either always or never get a college degree regardless of whether a local college exists.
Potential problems
Instrumental variables estimates are generally inconsistent if the instruments are correlated with the error term in the equation of interest. As Bound, Jaeger, and Baker (1995) note, another problem is caused by the selection of "weak" instruments, instruments that are poor predictors of the endogenous question predictor in the first-stage equation. In this case, the prediction of the question predictor by the instrument will be poor and the predicted values will have very little variation. Consequently, they are unlikely to have much success in predicting the ultimate outcome when they are used to replace the question predictor in the second-stage equation.
In the context of the smoking and health example discussed above, tobacco taxes are weak instruments for smoking if smoking status is largely unresponsive to changes in taxes. If higher taxes do not induce people to quit smoking (or not start smoking), then variation in tax rates tells us nothing about the effect of smoking on health. If taxes affect health through channels other than through their effect on smoking, then the instruments are invalid and the instrumental variables approach may yield misleading results. For example, places and times with relatively health-conscious populations may both implement high tobacco taxes and exhibit better health even holding smoking rates constant, so we would observe a correlation between health and tobacco taxes even if it were the case that smoking has no effect on health. In this case, we would be mistaken to infer a causal effect of smoking on health from the observed correlation between tobacco taxes and health.
Sampling properties and hypothesis testing
When the covariates are exogenous, the small-sample properties of the OLS estimator can be derived in a straightforward manner by calculating moments of the estimator conditional on X. When some of the covariates are endogenous so that instrumental variables estimation is implemented, simple expressions for the moments of the estimator cannot be so obtained. Generally, instrumental variables estimators only have desirable asymptotic, not finite sample, properties, and inference is based on asymptotic approximations to the sampling distribution of the estimator. Even when the instruments are uncorrelated with the error in the equation of interest and when the instruments are not weak, the finite sample properties of the instrumental variables estimator may be poor. For example, exactly identified models produce finite sample estimators with no moments, so the estimator can be said to be neither biased nor unbiased, the nominal size of test statistics may be substantially distorted, and the estimates may commonly be far away from the true value of the parameter.
Testing instrument strength and overidentifying restrictions
The strength of the instruments can be directly assessed because both the endogenous covariates and the instruments are observable. A common rule of thumb for models with one endogenous regressor is: the F-statistic against the null that the excluded instruments are irrelevant in the first-stage regression should be larger than 10.
The assumption that the instruments are not correlated with the error term in the equation of interest is not testable in exactly identified models. If the model is overidentified, there is information available which may be used to test this assumption. The most common test of these overidentifying restrictions, called the Sargan–Hansen test, is based on the observation that the residuals should be uncorrelated with the set of exogenous variables if the instruments are truly exogenous. The Sargan–Hansen test statistic can be calculated as
