Initial attractiveness - Alchetron, The Free Social Encyclopedia

The initial attractiveness is a possible extension of the Barabási–Albert model (preferential attachment model). The Barabási–Albert model generates scale-free networks where the degree distribution can be described by a pure power law. However, the degree distribution of most real life networks cannot be described by a power law solely. The most common discrepancies regarding the degree distribution found in real networks are the high degree cut-off (or structural cut-off) and the low degree cut-off. The inclusion of initial attractiveness in the Barabási–Albert model addresses the low-degree cut-off phenomenon.

Definition

The Barabási–Albert model defines the following linear preferential attachment rule: Π ( k i ) = k i ∑ j k j . This would imply that the probability that a new node will attach to a node that has a zero degree is zero – Π ( 0 ) = 0 . The preferential attachment function of the Barabási–Albert model can be modified as follows: Π ( k ) = A + k . The constant A denotes the initial attractiveness of the node. From this the preferential attachment rule with initial attractiveness comes as:

Π ( k i ) = A i + k i ∑ j ( A j + k j )

Based on this attachment rule it can be inferred that: Π ( 0 ) ∼ A . This means that even isolated nodes with Π ( 0 ) have a chance to obtain connections with the newly arriving nodes.

Consequences

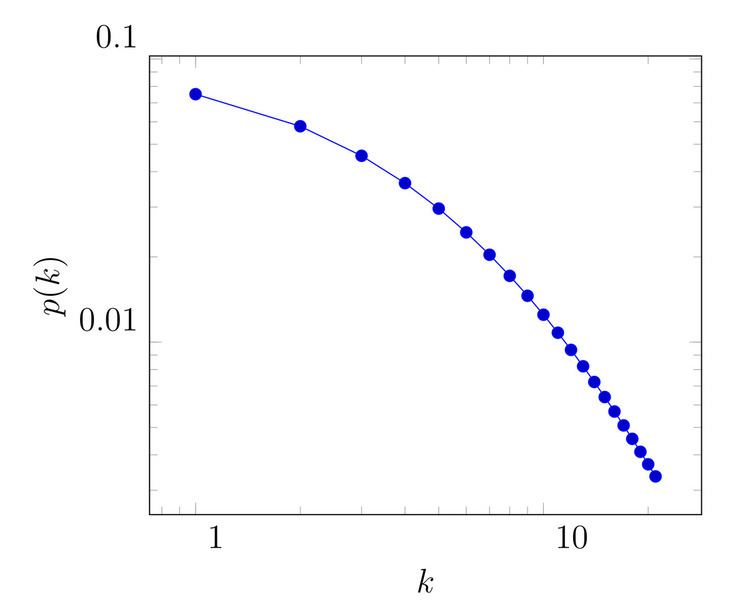
The presence of initial attractiveness results in two important consequences one is the small degree cut-off (or small degree saturation). The other on is the increased degree exponent of the degree distribution.

Small degree cut-off/saturation

The small degree saturation is an empirical regularity – the number of nodes with low degree is smaller than it would be expected if a power law would describe the degree distribution. The reason why this appears is the following: initial attractiveness increases the probability that the node obtains connection with an arriving node. This increased attachment probability becomes marginal as the node obtains more connections – it does not effect the right tail of the distribution. The degree distribution of a model with initial attractiveness can be described by the following: p k = C ⋅ ( k + A ) − γ .

Examples

There are numerous real life networks when the degree distribution shows some kind of small degree cut-off. The following list offers some examples:

Scientific collaboration network

Co-stardom network

Citation network

Higher degree exponent

Importantly, in case of the Barabási–Albert model the exponent of the degree distribution, here denoted by γ , has a value of 3. In case of the Barabási–Albert model with initial attractiveness the degree exponent is simply γ = 3 + A m . Here m denotes the initial number of links in the network. As γ is higher than 3 it follows that the network is in the random network regime and as the number of initial nodes is higher it converges to the scale-free regime. The same holds for the value of the initial attractiveness as A is higher the more the network is into the random network regime. This means that the number of nodes with relatively high degrees will be lower than it would be in the Barabási–Albert model. The higher degree exponent generally implies that the network is more homogeneous – most nodes are average linked.

References

Initial attractiveness Wikipedia

(Text) CC BY-SA