Influential observation

Assessment

Various methods have been proposed for measuring influence. Assume an estimated regression y = X b + e , where y is an n×1 column vector for the response variable, X is the n×k design matrix of explanatory variables (including a constant), e is the n×1 residual vector, and b is a k×1 vector of estimates of some population parameter β ∈ R k . Also define H ≡ X ( X T X ) − 1 X T , the projection matrix of X . Then we have the following measures of influence:

1. DFBETA i ≡ b − b ( − i ) = ( X T X ) − 1 x i T e i 1 − h i , where b ( − i ) denotes the coefficients estimated with the i-th row x i of X deleted, h i = x i ( X T X ) − 1 x i T denotes the i-th row of H . Thus DFBETA measures the difference in each parameter estimate with and without the influential point. There is a DFBETA for each point and each observation (if there are N points and k variables there are N·k DFBETAs).
2. DFFITS
3. Cook's D measures the effect of removing a data point on all the parameters combined.

Outliers, leverage and influence

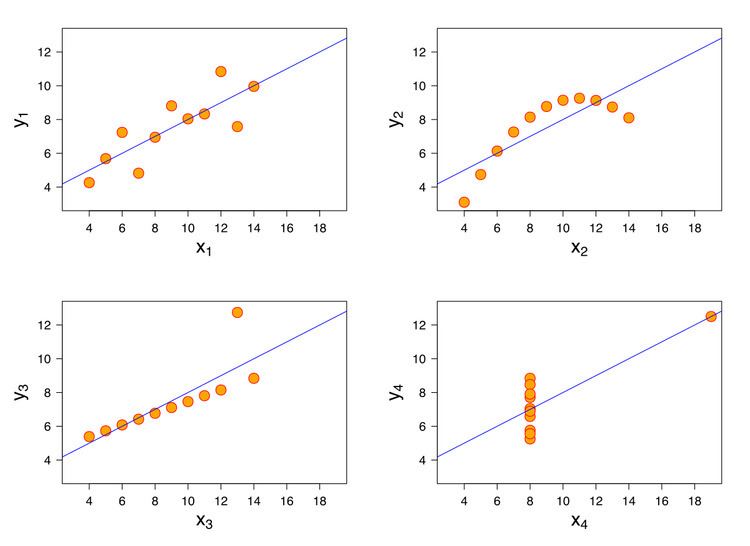
An outlier may be defined as a surprising data point. Leverage is a measure of how much the estimated value of the dependent variable changes when the point is removed. There is one value of leverage for each data point. Data points with high leverage force the regression line to be close to the point. In Anscombe's quartet, only the bottom right image has a point with high leverage.