 | ||
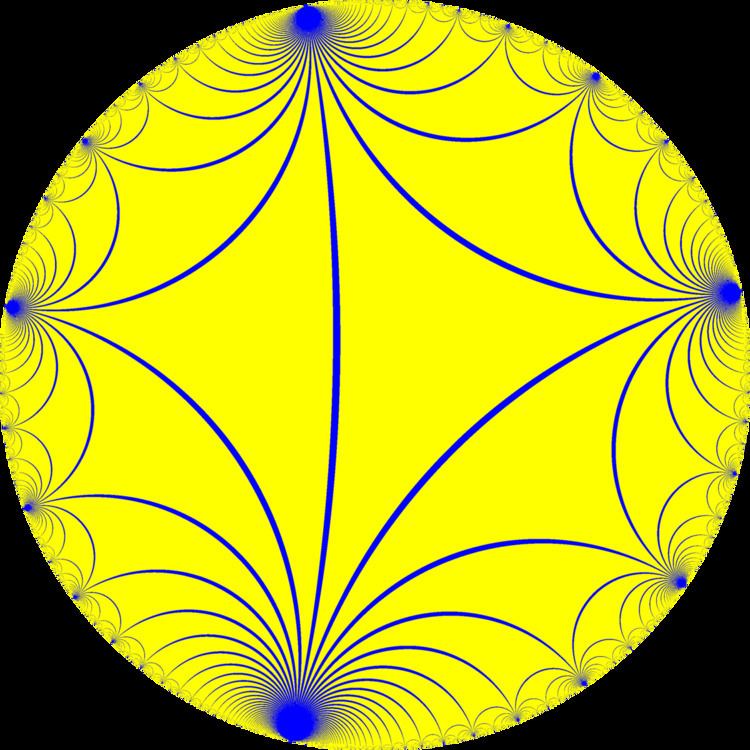
In geometry, the infinite-order triangular tiling is a regular tiling of the hyperbolic plane with a Schläfli symbol of {3,∞}. All vertices are ideal, located at "infinity" and seen on the boundary of the Poincaré hyperbolic disk projection.
Contents
Symmetry
A lower symmetry form has alternating colors, and represented by cyclic symbol {(3,∞,3)}, . The tiling also represents the fundamental domains of the *∞∞∞ symmetry, which can be seen with 3 colors of lines representing 3 mirrors of the construction.
Related polyhedra and tiling
This tiling is topologically related as part of a sequence of regular polyhedra with Schläfli symbol {3,p}.
Other infinite-order triangular tilings
A nonregular infinite-order triangular tiling can be generated by a recursive process from a central triangle as shown here:
References
Infinite-order triangular tiling Wikipedia(Text) CC BY-SA
