In phase and quadrature components

Definition

In vector analysis, a vector with polar coordinates A,φ and Cartesian coordinates x = A cos(φ), y = A sin(φ), can be represented as the sum of orthogonal "components": [x,0] + [0,y]. Similarly in trigonometry, the expression sin(x + φ) can be represented by sin(x) cos(φ) + sin(x + π/2) sin(φ). And in functional analysis, when x is a linear function of some variable, such as time, these components are sinusoids, and they are orthogonal functions. When φ = 0, sin(x + φ) reduces to just the in-phase component sin(x) cos(φ), and the quadrature component sin(x + π/2) sin(φ) is zero.

We now note that many authors prefer the identity cos(x + φ) = cos(x) cos(φ) + cos(x + π/2) sin(φ), in which case cos(x) cos(φ) is the in-phase component. In both conventions cos(φ) is the in-phase amplitude modulation, which explains why some authors refer to it as the actual in-phase component. We can also observe that in both conventions the quadrature component leads the in-phase component by one-quarter cycle.

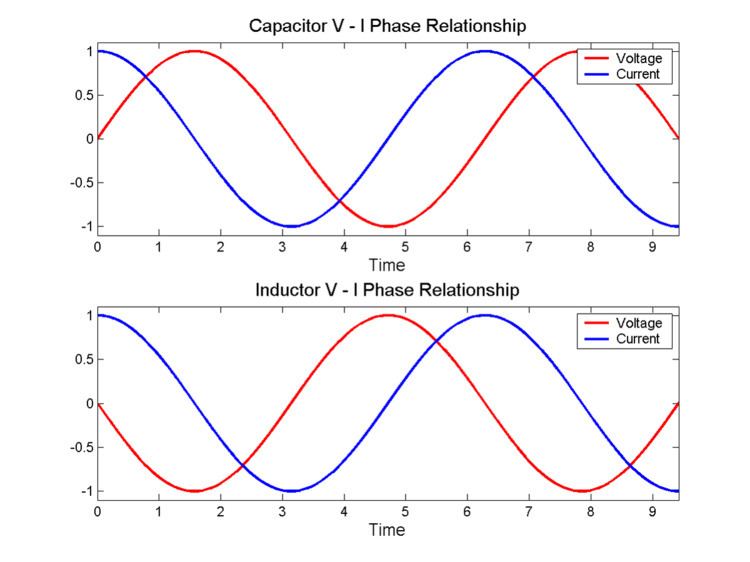
Alternating current (AC) circuits

The term alternating current applies to a voltage vs time function that is sinusoidal with a frequency, f ,   of 50 or 60 Hz. When it is applied to a typical circuit or device, it causes a current that is also sinusoidal. And in general there is a constant phase difference, φ, between the two sinusoids. The sinusoidal voltage stimulus is usually defined to have zero phase, meaning that it is arbitrarily chosen as a convenient time reference. So the phase difference is attributed to the current function, e.g.   sin ⁡ ( 2 π f t + φ ) ,   whose orthogonal components are   sin ⁡ ( 2 π f t ) cos ⁡ ( φ )   and   sin ⁡ ( 2 π f t + π / 2 ) sin ⁡ ( φ ) ,   as we have seen.  When φ happens to be such that the in-phase component is zero, the current and voltage sinusoids are said to be in quadrature, which means they are orthogonal to each other. In that case, no electrical power is consumed. Rather it is temporarily stored by the device and given back, once every 1 / f   seconds.  Note that the term in quadrature only implies that two sinusoids are orthogonal, not that they are components of another sinusoid.

Narrowband signal model

In an angle modulation application, with carrier frequency ƒ,  φ is also a time-variant function, giving:

When all three terms above are multiplied by an optional amplitude function, A(t) > 0,  the left-hand side of the equality is known as the amplitude/phase form, and the right-hand side is the quadrature-carrier or IQ form. Because of the modulation, the components are no longer completely orthogonal functions. But when A(t) and φ(t) are slowly varying functions compared to 2 π f t ,   the assumption of orthogonality is a common one. Authors often call it a narrowband assumption, or a narrowband signal model.  Orthogonality is important in many applications, including demodulation, direction-finding, and bandpass sampling.