 | ||
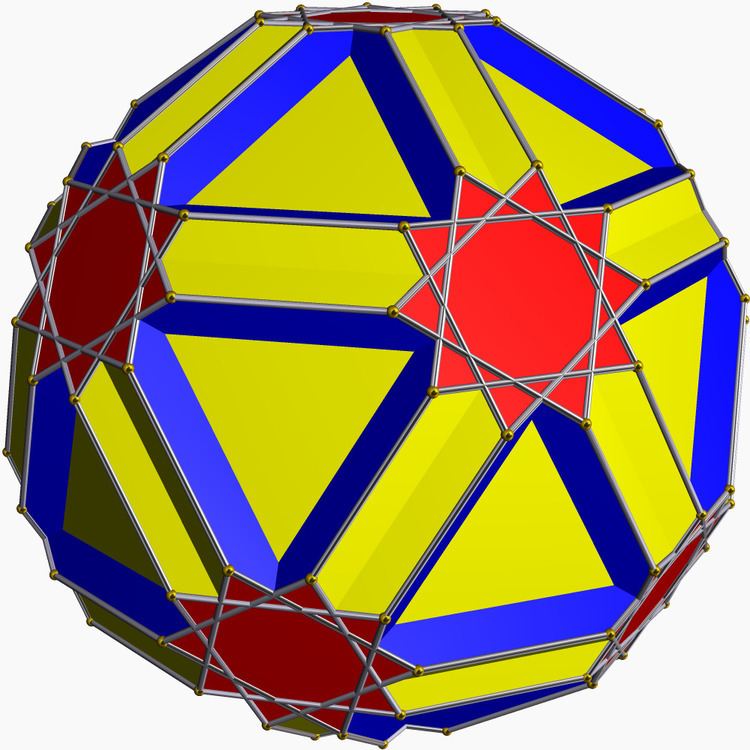
In geometry, the icositruncated dodecadodecahedron or icosidodecatruncated icosidodecahedron is a nonconvex uniform polyhedron, indexed as U45.
Contents
Convex hull
Its convex hull is a nonuniform truncated icosidodecahedron.
Cartesian coordinates
Cartesian coordinates for the vertices of an icositruncated dodecadodecahedron are all the even permutations of
(±(2−1/τ), ±1, ±(2+τ))(±1, ±1/τ2, ±(3τ−1))(±2, ±2/τ, ±2τ)(±3, ±1/τ2, ±τ2)(±τ2, ±1, ±(3τ−2))where τ = (1+√5)/2 is the golden ratio (sometimes written φ).
Tridyakis icosahedron
The tridyakis icosahedron is the dual polyhedron of the nonconvex uniform polyhedron, icositruncated dodecadodecahedron. It has 44 vertices, 180 edges, and 120 scalene triangular faces.
References
Icositruncated dodecadodecahedron Wikipedia(Text) CC BY-SA
