ISO 216

History

In 1786, the German scientist Georg Christoph Lichtenberg described the advantages of basing a paper size on an aspect ratio of 2 in a letter to Johann Beckmann. The formats that became ISO paper sizes A2, A3, B3, B4, and B5 were developed in France. They were listed in a 1798 law on taxation of publications that was based in part on page sizes.

The main advantage of this system is its scaling. Rectangular paper with an aspect ratio of 2 has the unique property that, when cut or folded in half midway between its shorter sides, each half has the same 2 aspect ratio and half the area of the whole sheet before it was divided. Equivalently, if one lays two same-sized sheets paper with an aspect ratio of 2 side-by-side along their longer side, they form a larger rectangle with the aspect ratio of 2 and double the area of each individual sheet.

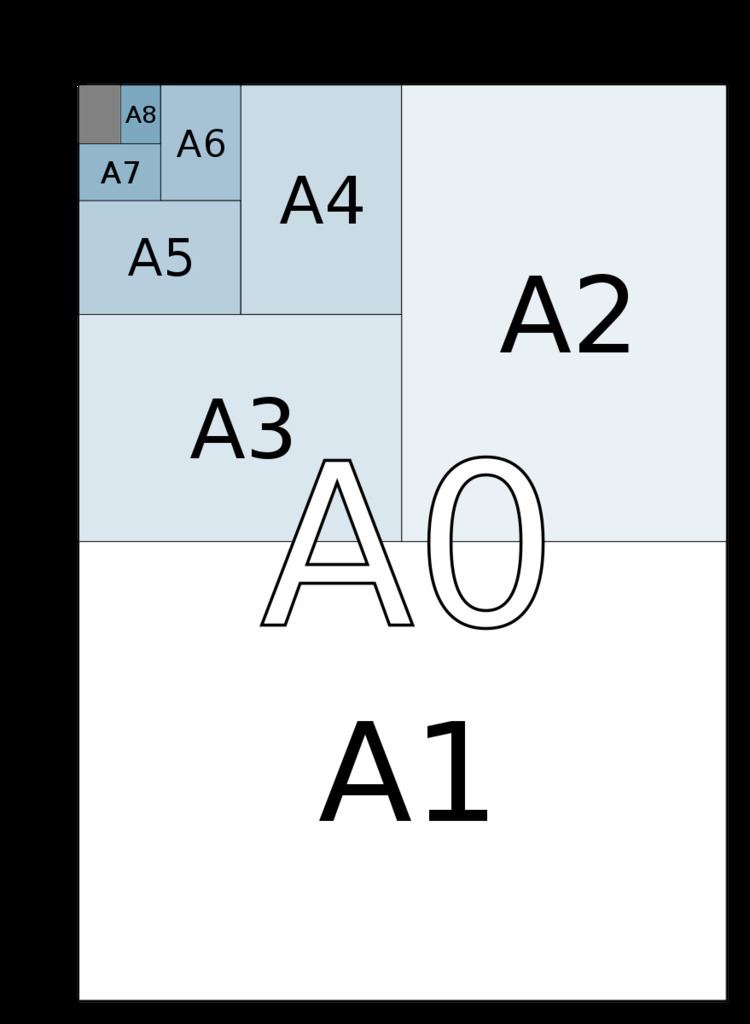
The ISO system of paper sizes exploit these properties of the 2 aspect ratio. In each series of sizes (for example, series A), the largest size is numbered 0 (for example, A0), and each successive size (for example, A1, A2, etc.) has half the area of the preceding sheet and can be cut by halving the length of the preceding size sheet. A folded brochure can be made by using a sheet of the next larger size (for example, an A4 sheet is folded in half to make a brochure with size A5 pages. An office photocopier or printer can be designed to reduce a page from A4 to A5 or to enlarge a page from A4 to A3. Similarly, two sheets of A4 can be scaled down to fit one A4 sheet without excess empty paper.

This system also simplifies calculating the weight paper. Under ISO 536, paper's grammage is defined as a sheet's weight in grams (g) per area in square metres (abbreviated g/m² or gsm). Since an A0 sheet has an area of 1 m², its weight in grams is the same as its grammage. One can derive the grammage of other sizes by arithmetic division in g/m². A standard A4 sheet made from 80 g/m² paper weighs 5 g, as it is  ¹⁄₁₆ (four halvings, ignoring roundings to exact mm) of an A0 page. Thus the weight, and the associated postage rate, can be easily approximated by counting the number of sheets used.

ISO 216 and its related standards were first published between 1975 and 1995:

A series

Paper in the A series format has a 2 ≈ 1.414 aspect ratio, rounded to the nearest millimetre. A0 is defined so that it has an area of 1 square metre before rounding. Successive paper sizes in the series (A1, A2, A3, etc.) are defined by halving the length of the preceding paper size, so that the long side of A ( n + 1 ) is the same length as the short side of A n before rounding.

The most frequently used of this series is the size A4 which is 210 mm × 297 mm (8.27 in × 11.7 in) and so almost 1 16 square metres in area. For comparison, the letter paper size commonly used in North America (8.5 in × 11 in (216 mm × 279 mm)) is approximately 6 mm (0.24 in) wider and 18 mm (0.71 in) shorter than A4.

The geometric rationale behind the square root of 2 is to maintain the aspect ratio of each subsequent rectangle after cutting or folding an A series sheet in half, perpendicular to the larger side. Given a rectangle with a longer side, x, and a shorter side, y, ensuring that its aspect ratio, x y , will be the same as that of a rectangle half its size, y x / 2 , means that x y = y x / 2 , which reduces to x y = 2 ; in other words, an aspect ratio of 1 : 2 .

The formula that gives the larger border of the paper size An in metres and without rounding off is the geometric sequence: a n = 2 1 4 − n 2 . The paper size An thus has the dimension a n × a n + 1 and area (before rounding off) 2 − n m 2 .

The exact millimetre measurement of the long side of An is given by ⌊ 1000 / ( 2 2 n − 1 4 ) + 0.2 ⌋ , in which the modified brackets represent the floor function.

B series

The B series is defined in the standard as follows: "A subsidiary series of sizes is obtained by placing the geometrical means between adjacent sizes of the A series in sequence." The use of the "geometric means", means that each step in size: B0, A0, B1, A1, B2 … is smaller than the previous by an equal scaling. As with the A series, the lengths of the B series have the ratio 1:√2, and folding one in half gives the next in the series. The shorter side of B0 is exactly 1 metre.

There is also an incompatible Japanese B series which the JIS defines to have 1.5 times the area of the corresponding JIS A series (which is identical to the ISO A series). Thus, the lengths of JIS B series paper are 1.5 ≈ 1.22 times those of A-series paper. By comparison, the lengths of ISO B series paper are 2 4 ≈ 1.19 times those of A-series paper.

For the ISO B series, the exact millimetre measurement of the long side of Bn is given by ⌊ 1000 / ( 2 n − 1 2 ) + 0.2 ⌋ .

C series

The C series formats are geometric means between the B series and A series formats with the same number (e.g., C2 is the geometric mean between B2 and A2). The width to height ratio is as in the A and B series. The C series formats are used mainly for envelopes. An A4 page will fit into a C4 envelope. C series envelopes follow the same ratio principle as the A series pages. For example, if an A4 page is folded in half so that it is A5 in size, it will fit into a C5 envelope (which will be the same size as a C4 envelope folded in half). The lengths of ISO C series paper are therefore ⁸√2 times those of A-series paper – i.e., about 9% larger.

A, B, and C paper fit together as part of a geometric progression, with ratio of successive side lengths of ⁸√2, though there is no size half-way between Bn and A(n − 1): A4, C4, B4, "D4", A3, …; there is such a D-series in the Swedish extensions to the system.

The exact millimetre measurement of the long side of Cn is given by ⌊ 1000 / ( 2 4 n − 3 8 ) + 0.2 ⌋ .

Tolerances

The tolerances specified in the standard are:

These are related to comparison between series A, B and C.

Application

The ISO 216 formats are organized around the ratio 1:√2; two sheets next to each other together have the same ratio, sideways. In scaled photocopying, for example, two A4 sheets reduced to A5 size fit exactly onto one A4 sheet, and an A4 sheet in magnified size onto an A3 sheet; in each case, there is neither waste nor want.

The principal countries not generally using the ISO paper sizes are the United States and Canada, which use the Letter, Legal and Executive system. Although they have also officially adopted the ISO 216 paper format, Mexico, Panama, Venezuela, Colombia, the Philippines, and Chile also use mostly U.S. paper sizes.

Rectangular sheets of paper with the ratio 1:√2 are popular in paper folding, such as origami, where they are sometimes called "A4 rectangles" or "silver rectangles". In other contexts, the term "silver rectangle" can also refer to a rectangle in the proportion 1:(1 + √2), known as the silver ratio.