I bundle

In mathematics, an I-bundle is a fiber bundle whose fiber is an interval and whose base is a manifold. Any kind of interval, open, closed, semi-open, semi-closed, open-bounded, compact, even rays, can be the fiber.

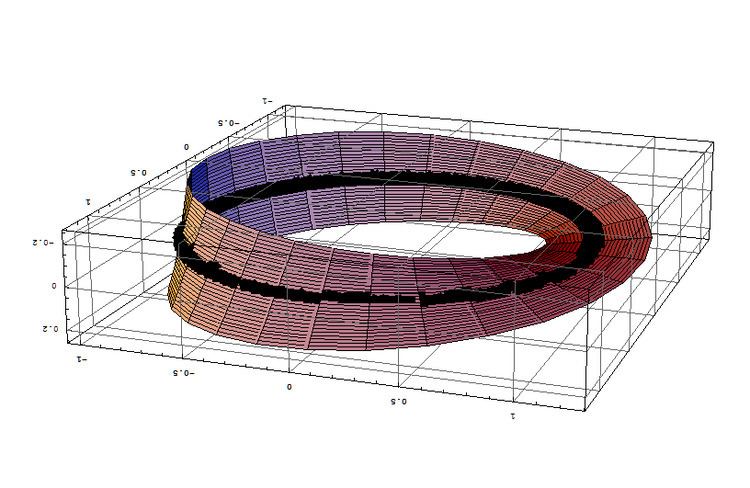
Two simple examples of I-bundles are the annulus and the Möbius band, the only two possible I-bundles over the circle S 1 . The annulus is a trivial or untwisted bundle because it corresponds to the Cartesian product S 1 × I , and the Möbius band is a non-trivial or twisted bundle. Both bundles are 2-manifolds, but the annulus is an orientable manifold while the Möbius band is a non-orientable manifold.

Curiously, there are only two kinds of I-bundles when the base manifold is any surface but the Klein bottle K . That surface has three I-bundles: the trivial bundle K × I and two twisted bundles.

Together with the Seifert fiber spaces, I-bundles are fundamental elementary building blocks for the description of three-dimensional spaces. These observations are simple well known facts on elementary 3-manifolds.

Line bundles are both I-bundles and vector bundles of rank one. When considering I-bundles, one is interested mostly in their topological properties and not their possible vector properties, as we might be for line bundles.