 | ||
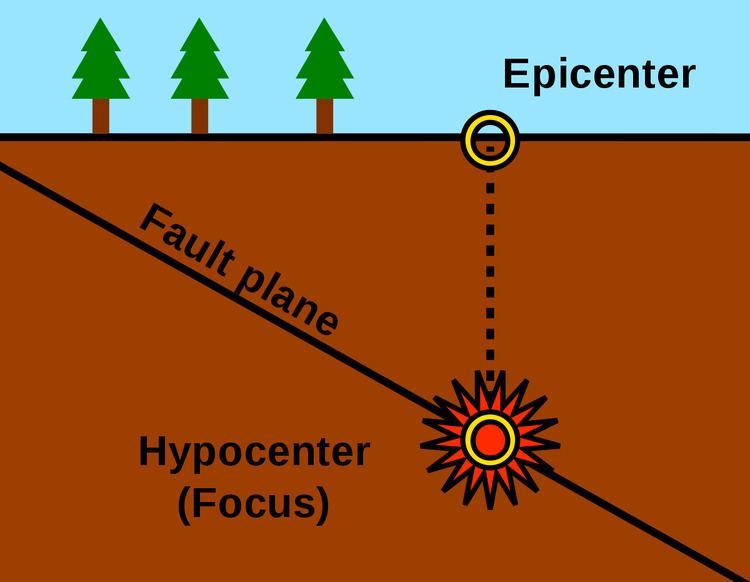
A hypocenter (or hypocentre) (from Ancient Greek: ὑπόκεντρον [hypόkentron] for 'below the center') is the point of origin of an earthquake or a subsurface nuclear explosion. It is a synonym of the focus. Confusingly, the term hypocenter is also used as a synonym for ground zero, the surface point directly beneath a nuclear airburst.
Earthquakes
An earthquake's hypocenter is the position where the strain energy stored in the rock is first released, marking the point where the fault begins to rupture. This occurs directly beneath the epicenter, at a distance known as the focal or hypocentral depth.
The focal depth can be calculated from measurements based on seismic wave phenomena. As with all wave phenomena in physics, there is uncertainty in such measurements that grows with the wavelength so the focal depth of the source of these long-wavelength (low frequency) waves is difficult to determine exactly. Very strong earthquakes radiate a large fraction of their released energy in seismic waves with very long wavelengths and therefore a stronger earthquake involves the release of energy from a larger mass of rock.
Computing the hypocenters of foreshocks, main shock, and aftershocks of earthquakes allows the three-dimensional plotting of the fault along which movement is occurring. The expanding wavefront from the earthquake's rupture propagates at a speed of several kilometers per second, this seismic wave is what is measured at various surface points in order to geometrically determine an initial guess as to the hypocenter. The wave reaches each station based upon how far away it was from the hypocenter. A number of things need to be taken into account, most importantly variations in the waves speed based upon the materials that it is passing through. With adjustments for velocity changes, the initial estimate of the hypocenter is made, then a series of linear equations is set up, one for each station. The equations express the difference between the observed arrival times and those calculated from the initial estimated hypocenter. These equations are solved by the method of least squares which minimizes the sum of the squares of the differences between the observed and calculated arrival times, and a new estimated hypocenter is computed. The system iterates until the location is pinpointed within the margin of error for the velocity computations; this is known as linear regression.
