Puneet Varma (Editor)

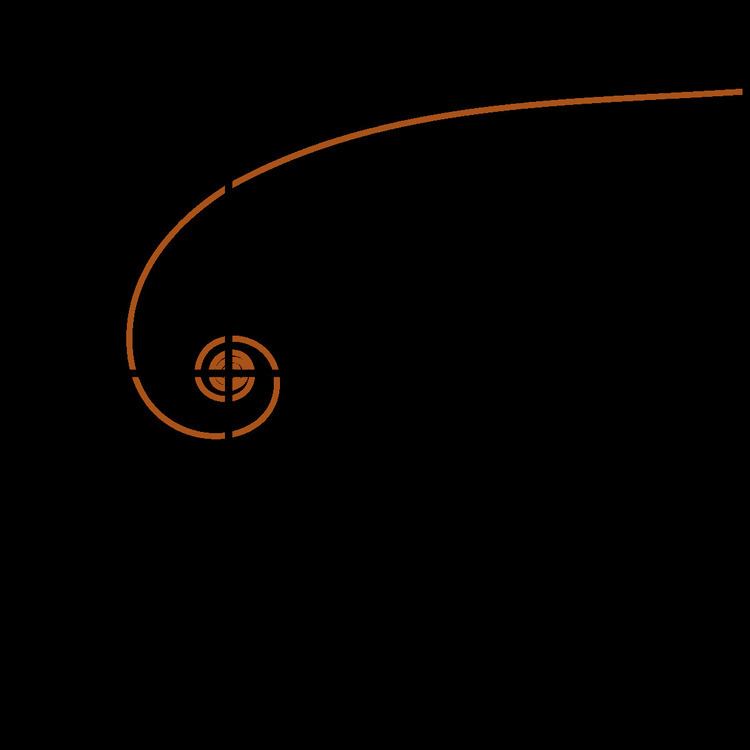
Hyperbolic spiral

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Hyperbolic spiral

A hyperbolic spiral is a transcendental plane curve also known as a reciprocal spiral. A hyperbolic spiral is the opposite of an Archimedean spiral and is a type of Cotes' spiral.

Contents

Pierre Varignon first studied the curve in 1704. Later Johann Bernoulli and Roger Cotes worked on the curve as well.

Equation

The hyperbolic spiral has the polar equation:

r = a θ

It begins at an infinite distance from the pole in the center (for θ starting from zero r = a/θ starts from infinity), and it winds faster and faster around as it approaches the pole; the distance from any point to the pole, following the curve, is infinite. Applying the transformation from the polar coordinate system:

x = r cos ⁡ θ , y = r sin ⁡ θ ,

leads to the following parametric representation in Cartesian coordinates:

x = a cos ⁡ t t , y = a sin ⁡ t t ,

where the parameter t is an equivalent of the polar coordinate θ.

Asymptote

The spiral has an asymptote at y = a: for t approaching zero the ordinate approaches a, while the abscissa grows to infinity:

lim t → 0 x = a lim t → 0 cos ⁡ t t = ∞ , lim t → 0 y = a lim t → 0 sin ⁡ t t = a ⋅ 1 = a .

Curvature

Using the representation of the hyperbolic spiral in polar coordinates, the curvature can be found by

κ = r 2 + 2 r θ 2 − r r θ θ ( r 2 + r θ 2 ) 3 / 2

where

r θ = d r d θ = − a θ 2

and

r θ θ = d 2 r d θ 2 = 2 a θ 3 .

Then the curvature at θ reduces to

κ ( θ ) = θ 4 a ( θ 2 + 1 ) 3 / 2 .

The curvature tends to infinity as θ tends to infinity. For values of θ between 0 and 1, the curvature increases exponentially, and for values greater than 1, the curvature increases at an approximately linear rate with respect to the angle.

Tangents

The polar tangential angle of the hyperbolic spiral is

ψ ( θ ) = − arctan ⁡ θ .

References

Hyperbolic spiral Wikipedia
(Text) CC BY-SA