 | ||
In triangle geometry, a Hofstadter point is a special point associated with every plane triangle. In fact there are several Hofstadter points associated with a triangle. All of them are triangle centers. Two of them, the Hofstadter zero-point and Hofstadter one-point, are particularly interesting. They are two transcendental triangle centers. Hofstadter zero-point is the center designated as X(360) and the Hofstafter one-point is the center denoted as X(359) in Clark Kimberling's Encyclopedia of Triangle Centers. The Hofstadter zero-point was discovered by Douglas Hofstadter in 1992.
Contents
Hofstadter triangles
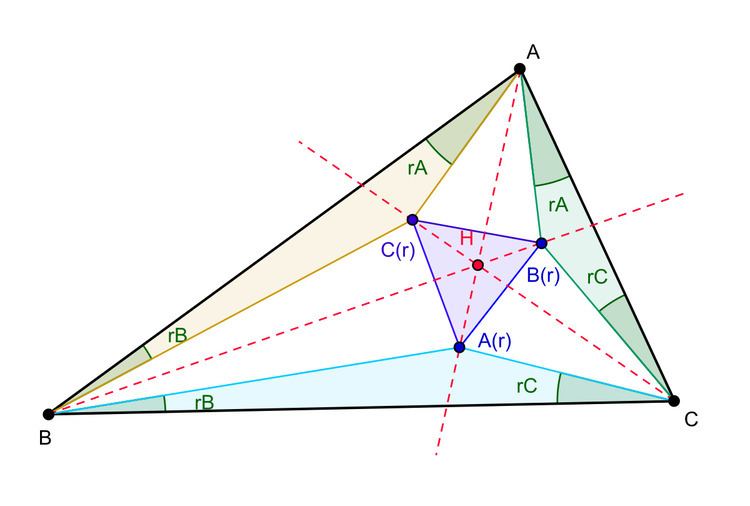
Let ABC be a given triangle. Let r be a positive real constant.
Rotate the line segment BC about B through an angle rB towards A and let LBC be the line containing this line segment. Next rotate the line segment BC about C through an angle rC towards A. Let L'BC be the line containing this line segment. Let the lines LBC and L'BC intersect at A(r). In a similar way the points B(r) and C(r) are constructed. The triangle whose vertices are A(r), B(r), C(r) is the Hofstadter r-triangle (or, the r-Hofstadter triangle) of triangle ABC.
Special case
Trilinear coordinates of the vertices of Hofstadter triangles
The trilinear coordinates of the vertices of the Hofstadter r-triangle are given below:
A(r) = ( 1 , sin rB / sin (1 − r)B , sin rC / sin (1 − r)C )B(r) = ( sin rA / sin (1 − r)A , 1 , sin rC / sin (1 − r)C )C(r) = ( sin rA / sin (1 − r)A , sin (1 − r)B / sin rB , 1 )Hofstadter points
For a positive real constant r > 0, let A(r) B(r) C(r) be the Hofstadter r-triangle of triangle ABC. Then the lines AA(r), BB(r), CC(r) are concurrent. The point of concurrence is the Hofstdter r-point of triangle ABC.
Trilinear coordinates of Hofstadter r-point
The trilinear coordinates of Hofstadter r-point are given below.
( sin rA / sin ( A − rA) , sin rB / sin ( B − rB ) , sin rC / sin ( C − rC) )Hofstadter zero- and one-points
The trilinear coordinates of these points cannot be obtained by plugging in the values 0 and 1 for r in the expressions for the trilinear coordinates for the Hofstdter r-point.
Hofstadter zero-point is the limit of the Hofstadter r-point as r approaches zero.Hofstadter one-point is the limit of the Hofstadter r-point as r approaches one.Trilinear coordinates of Hofstadter zero-point
= lim r → 0 ( sin rA / sin ( A − rA) , sin rB / sin ( B − rB ) , sin rC / sin ( C − rC) )= lim r → 0 ( sin rA / r sin ( A − rA) , sin rB / r sin ( B − rB ) , sin rC / r sin ( C − rC) )= lim r → 0 ( A sin rA / rA sin ( A − rA) , B sin rB / rB sin ( B − rB ) , C sin rC / rC sin ( C − rC) )= ( A / sin A , B / sin B , C / sin C ) ), as lim r → 0 sin rA / rA = 1, etc.= ( A / a, B / b, C / c )Trilinear coordinates of Hofstadter one-point
= lim r → 1 ( sin rA / sin ( A − rA) , sin rB / sin ( B − rB ) , sin rC / sin ( C − rC) )= lim r → 1 ( ( 1 − r ) sin rA / sin ( A − rA) , ( 1 - r ) sin rB / sin ( B − rB ) , ( 1 − r )sin rC / sin ( C − rC) )= lim r → 1 ( ( 1 − r ) A sin rA / A sin ( A − rA) , ( 1 − r ) B sin rB / B sin ( B − rB ) , ( 1 − r ) C sin rC / C sin ( C − rC) )= ( sin A / A , sin B / B , sin C / C ) ) as lim r → 1 ( 1 − r ) A / sin ( A − rA ) = 1, etc.= ( a / A, b / B, c / C )