 | ||
In biomechanics, Hill's muscle model refers to either Hill's equations for tetanized muscle contraction or to the 3-element model. They were derived by the famous physiologist Archibald Vivian Hill.
Contents
AnimatLab Hill Muscle Model
Equation to tetanized muscle
This is a popular state equation applicable to skeletal muscle that has been stimulated to show Tetanic contraction. It relates tension to velocity with regard to the internal thermodynamics. The equation is
where
Although Hill's equation looks very much like the van der Waals equation, the former has units of energy dissipation, while the latter has units of energy. Hill's equation demonstrates that the relationship between F and v is hyperbolic. Therefore, the higher the load applied to the muscle, the lower the contraction velocity. Similarly, the higher the contraction velocity, the lower the tension in the muscle. This hyperbolic form has been found to fit the empirical constant only during isotonic contractions near resting length.
The muscle tension decreases as the shortening velocity increases. This feature has been attributed to two main causes. The major appears to be the loss in tension as the cross bridges in the contractile element and then reform in a shortened condition. The second cause appears to be the fluid viscosity in both the contractile element and the connective tissue. Whichever the cause of loss of tension, it is a viscous friction and can therefore be modeled as a fluid damper .
Three-element model
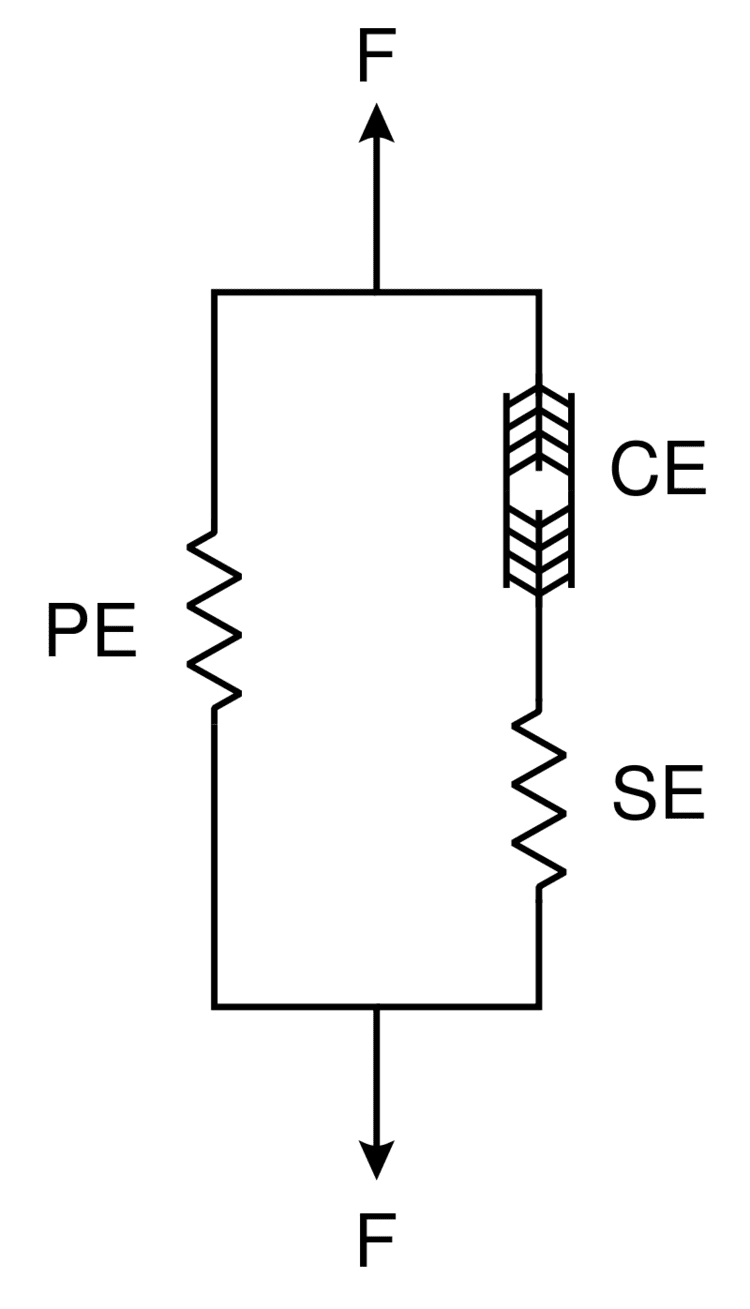
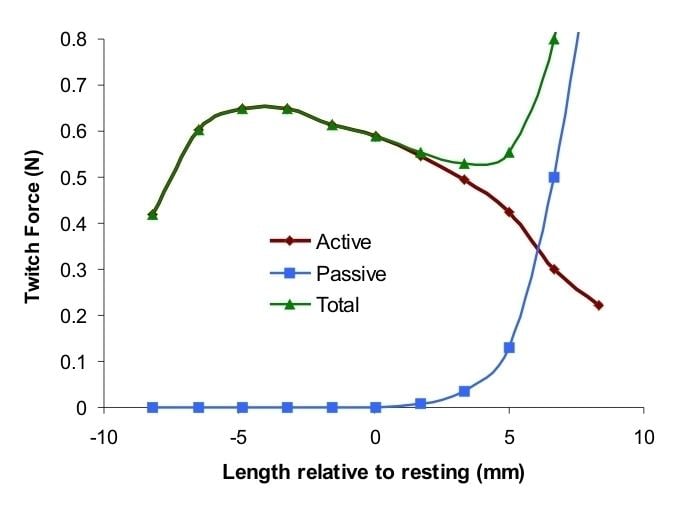
The three-element Hill muscle model is a representation of the muscle mechanical response. The model is constituted by a contractile element (CE) and two non-linear spring elements, one in series (SE) and another in parallel (PE). The active force of the contractile element comes from the force generated by the actin and myosin cross-bridges at the sarcomere level. It is fully extensible when inactive but capable of shortening when activated. The connective tissues (fascia, epimysium, perimysium and endomysium) that surround the contractile element influences the muscle's force-length curve. The parallel element represents the passive force of these connective tissues and has a soft tissue mechanical behavior. The parallel element is responsible for the muscle passive behavior when it is stretched, even when the contractile element is not activated. The series element represents the tendon and the intrinsic elasticity of the myofilaments. It also has a soft tissue response and provides energy storing mechanism.
The net force-length characteristics of a muscle is a combination of the force-length characteristics of both active and passive elements. The forces in the contractile element, in the series element and in the parallel element,
On the other hand, the muscle length
During isometric contractions the series elastic component is under tension and therefore is stretched a finite amount. Because the overall length of the muscle is kept constant, the stretching of the series element can only occur if there is an equal shortening of the contractile element itself.
Viscoelasticity
Muscles present viscoelasticity, therefore a viscous damper may be included in the model, when the dynamics of the second-order critically damped twitch is regarded. One common model for muscular viscosity is an exponential form damper, where
is added to the model's global equation, whose
