Years active 1942–present Age range 8+ to adult | Players 2 Setup time None | |
 | ||
Genre(s) Board gameAbstract strategy gameConnection game Playing time | ||
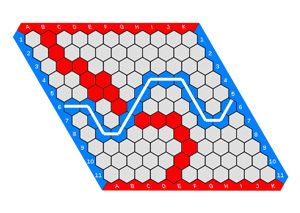
Hex is a strategy board game for two players played on a hexagonal grid, theoretically of any size and several possible shapes, but traditionally as an 11×11 rhombus. Players alternate placing markers or stones (Go stones make ideal playing pieces) on unoccupied spaces in an attempt to link their opposite sides of the board in an unbroken chain. One player must win; there are no draws. The game has deep strategy, sharp tactics and a profound mathematical underpinning related to the Brouwer fixed point theorem. It was invented in the 1940s independently by two mathematicians. The game was first marketed as a board game in Denmark under the name Con-tac-tix, and Parker Brothers marketed a version of it in 1952 called Hex; they are no longer in production. Hex can also be played with paper and pencil on hexagonally ruled graph paper.
Contents
- Game type
- Published games
- Shannons hex machine
- Research
- Automatons
- Rules
- Strategy
- Theory and proofs
- Complexity
- Variants
- Rectangular grids and paper and pencil
- Board sizes
- Reverse hex
- Blockbusters
- Y
- Havannah
- Competition
- References
Hex-related research is current in the areas of topology, graph and matroid theory, combinatorics, game theory and computer heuristics.
Game type
Hex is a connection game, and can be classified as a Maker-Breaker game, a particular type of positional game. The game can never end in a draw (tie), in other words, Hex is also a "determined game".
Hex is a finite, perfect information game, and an abstract strategy game that belongs to the general category of "connection" games. When played on a generalized graph, it is equivalent to the Shannon switching game.
As a product, Hex is a board game; it may also be played with paper and pencil.
Published games
The game was invented by the Danish mathematician Piet Hein, who introduced it in 1942 at the Niels Bohr Institute. Although Hein called it Con-tac-tix, it became known in Denmark under the name Polygon due to an article by Hein in the December 26, 1942 edition of the Danish newspaper Politiken, the first published description of the game, in which he used that name. The game was independently re-invented in 1948 by the mathematician John Nash at Princeton University; Nash's fellow players at first called the game Nash. According to Martin Gardner, who featured Hex in his July 1957 Mathematical Games column, some of the Princeton University students also referred to the game as John (according to some sources this was because they played the game using the mosaic of the bathroom floor). In 1952, Parker Brothers marketed a version. They called their version "Hex" and the name stuck. Hex was also issued as one of the games in the 1974 3M Paper Games Series; the game contained a 5½ × 8½ inch 50-sheet pad of ruled hex grids.
Shannon's hex machine
About 1950, American mathematician and electrical engineer Claude Shannon and E. F. Moore constructed an analog Hex playing machine, which was essentially a resistance network with resistors for edges and lightbulbs for vertices. The move to be made corresponded to a certain specified saddle point in the network. The machine played a reasonably good game of Hex. Later, researchers attempting to solve the game and develop hex-playing computer algorithms, emulated Shannon's network to make strong automatons.
Research
In 1952 John Nash expounded an existence proof that on symmetrical boards, the first player has a winning strategy.
In 1964, mathematician Alfred Lehman showed that Hex cannot be represented as a binary matroid, so a determinate winning strategy like that for the Shannon switching game on a regular rectangular grid, was unavailable. The game was later shown to be PSPACE-complete.
In 2002, the first explicit winning strategy (a reduction-type strategy) on a 7x7 board was described.
In the 2000's, by using brute force search computer algorithms, Hex boards up to size 9x9 (as of 2016) have been completely solved.
Automatons
Various paradigms resulting from research into the game have been used to create digital computer Hex playing automatons starting about 2000. The first implementations used evaluation functions that emulated Shannon and Moore's electrical circuit model embedded in an alpha-beta search framework with hand-crafted knowledge-based patterns. Starting about 2006, Monte Carlo tree search methods borrowed from successful computer implementations of Go were introduced and soon dominated the field. Later, hand crafted patterns were supplemented by machine learning methods for pattern discovery. These programs are now competitive against skilled human players. Elo based ratings have been assigned to the various programs and can be used to measure technical progress as well as assess playing strength against Elo-rated humans. Current research is often published in either the quarterly ICGA Journal or the annual Advances in Computer Games series (van den Herik et.al. eds.).
Rules
Each player has an allocated color, conventionally Red and Blue or White and Black. Players take turns placing a stone of their color on a single cell within the overall playing board. The goal for each player is to form a connected path of their own stones linking the opposing sides of the board marked by their colors, before their opponent connects his or her sides in a similar fashion. The first player to complete his or her connection wins the game. The four corner hexagons each belong to both adjacent sides.
Since the first player to move in Hex has a distinct advantage, the pie rule is generally implemented for fairness. This rule allows the second player to choose whether to switch positions with the first player after the first player makes the first move.
Strategy
From the proof of a winning strategy for the first player, it is known that the hex board must have a complex type of connectivity which has never been solved. Play consists of creating small patterns which have a simpler type of connectivity called "safely connected", and joining them into sequences that form a "path". Eventually, one of the players will succeed in forming a safely connected path of stones and spaces between his sides of the board and win. The final stage of the game, if necessary, consists of filling in the empty spaces in the path.
A "safely connected" pattern is composed of stones of the player's color and open spaces which can be joined into a chain, an unbroken sequence of edge-wise adjacent stones, no matter how the opponent plays. One of the simplest such patterns is the bridge see (diagram 1), which consists of two stones of the same color (A and C), and a pair of open spaces (B and D). If the opponent plays in either space, the player plays in the other, creating a contiguous chain. There are also safely connected patterns which connect stones to edges. One such pattern, analogous to the bridge, is shown in diagram 2. There are many more safely connected patterns, some quite complex, built up of simpler ones like those shown. Patterns and paths can be disrupted by the opponent before they are complete, so the configuration of the board during an actual game often looks like a patchwork rather than something planned or designed.
There are weaker types of connectivity than "safely connected" which exist between stones or between safely connected patterns which have multiple spaces between them. The middle part of the game consists of creating a network of such weakly connected stones and patterns which hopefully will allow the player, by filling in the weak links, to construct just one safely connected path (see diagram 3) between sides as the game progresses.
Success at hex requires a particular ability to visualize synthesis of complex patterns in a heuristic way, and estimating whether such patterns are 'strongly enough' connected to enable an eventual win. The skill is somewhat similar to the visualization of patterns, sequencing of moves, and evaluating of positions in chess.
Theory and proofs
John Nash was the first to prove (circa 1949) that Hex cannot end in a draw, a non-trivial result colloquially called the "Hex theorem", which we now know is equivalent to the Brouwer fixed-point theorem. Apparently, he didn't publish the proof. The first exposition of it appears in an an in-house technical report in 1952.
There is a reductio ad absurdum existence proof attributed to John Nash circa 1949 that the first player in Hex on a board of any size has a winning strategy. Such a proof gives no indication of a correct strategy for play. The proof is common to a number of games including Hex, and has come to be called the "strategy-stealing" argument. Here is a highly condensed informal statement of the proof:
1. Either the first or second player must win, therefore there must be a winning strategy for either the first or second player.
2. Let us assume that the second player has a winning strategy.
3. The first player can now adopt the following defense. He makes an arbitrary move. Thereafter he plays the winning second player strategy assumed above. If in playing this strategy, he is required to play on the cell where an arbitrary move was made, he makes another arbitrary move. In this way he plays the winning strategy with one extra piece always on the board.
4. This extra piece cannot interfere with the first player's imitation of the winning strategy, for an extra piece is always an asset and never a handicap. Therefore the first player can win.
5. Because we have now contradicted our assumption that there is a winning strategy for the second player, we are forced to drop this assumption.
6. Consequently, there must be a winning strategy for the first player.
In 1976, Shimon Even and Robert Tarjan proved that determining whether a position in a game of generalized Hex played on arbitrary graphs is a winning position is PSPACE-complete. A strengthening of this result was proved by Reisch by reducing quantified Boolean formula in conjunctive normal form to Hex played on arbitrary planar graphs. In computational complexity theory, it is widely conjectured that PSPACE-complete problems cannot be solved with efficient (polynomial time) algorithms. This result limits the efficiency of the best possible algorithms when considering arbitrary positions on boards of unbounded size, but it doesn't rule out the possibility of a simple winning strategy for the initial position (on boards of unbounded size), or a simple winning strategy for all positions on a board of a particular size.
In 2002, Jing Yang, Simon Liao and Mirek Pawlak found an explicit winning strategy for the first player on Hex boards of size 7×7 using a decomposition method with a set of reusable local patterns. They extended the method to weakly solve the center pair of topologically congruent openings on 8×8 boards in 2002 and the center opening on 9×9 boards in 2003. In 2009, Philip Henderson, Broderick Arneson and Ryan B. Hayward completed the analysis of the 8×8 board with a computer search, solving all the possible openings. In 2013, Jakub Pawlewicz and Ryan B. Hayward solved all openings for 9×9 boards, and one opening move on the 10×10 board.
The determinacy of Hex has other mathematical consequences: it can be used to prove the two-dimensional Brouwer fixed point theorem, as David Gale showed in 1979, and the determinacy of higher-dimensional variants proves the fixed-point theorem in general.
Complexity
In 11x11 Hex, there are approx. 2.4x1056 possible legal positions; this compares to 4.6x1046 legal positions in chess.
A rough estimate of the number of nodes in the game tree can be obtained as an exponential function of the average branching factor and the average number of plies in a game thus: bd where d is the ply depth and b is the branching factor. In Hex, the average branching factor is a function of the ply depth. It has been stated that the average branching factor is about 100; that implies an average ply depth of 43 (there will be 121 open spaces on the board when the first player is to make his first move, and 79 when he is to make his 22nd move, the 43rd ply - the average number of open spaces, i.e. branching factor, during the game is (121+120+...+79)/43=100). Therefore the game tree size has an upper bound of approx. 10043 = 1086. The bound includes some number of illegal positions due to playing on when there is a complete chain for one player or the other, as well as excludes legal positions for games longer than 43 ply. Another researcher obtained a state space estimate of 1057 and a game tree size of 1098 using an upper limit of 50 plies for the game. This compares to 10123 node game tree size of chess.
An interesting reduction is available by noting that the board has rotational symmetry: for each position, a topologically identical position is obtained by rotating the board 1800.
Variants
Other connection games with similar objectives but different structures include Shannon switching game and TwixT. All of these games bear varying degrees of similarity to the ancient Asian game of Go.
Rectangular grids and paper and pencil
The game may be played on a rectangular grid like a chess, checker or go board, by considering that spaces (intersections in the case of go) are connected in one diagonal direction but not the other. The game may be played with paper and pencil on a rectangular array of dots or graph paper in the same way by using two different colored pencils.
Board sizes
Popular dimensions other than the standard 11x11 are 13×13 and 19×19 as a result of the game's relationship to the older game of Go. According to the book A Beautiful Mind, John Nash (one of the game's inventors) advocated 14×14 as the optimal size.
Reverse hex
A variation has been described in which each player tries to force his opponent to make a chain. This is a slow game. A clever proof has been discovered that the first player can win on a board with an even number of cells per side, and the second player can win on a board with an odd number.
Blockbusters
Hex had an incarnation as the question board from the television game show Blockbusters. In order to play a "move", contestants had to answer a question correctly. The board had 5 alternating columns of 4 hexagons; the solo player could connect top-to-bottom in 4 moves, while the team of two could connect left-to-right in 5 moves.
Y
The game of Y is Hex played on a triangular grid of hexagons; the object is for either player to connect all three sides of the triangle. Y is a generalization of Hex to the extent that any position on a Hex board can be represented as an equivalent position on a larger Y board.
Havannah
Havannah is a rather broadly defined variant of Hex played on a hexagonal grid of hexagons. The objective is for either player to complete one of three characteristic patterns.
Competition
As of 2016, there were over-the-board tournaments reported from Brazil (Catalão GO), Czech Republic (Praha), Denmark (Odense), France (Cannes, Le Mans, Neufchâtel-en-Bray, Paris), Germany (Leipzig, Sinzig), Italy (Genova, Pisa), Netherlands (Hilversum, Tiel), Norway (Oslo), Poland (Breslau), Portugal (Aljezur, Alpedrinha, Amaraleja, Amares, Arcos de Valdevez, Aveiro, Barreiro, Batalha, Braga, Cacém-Agualva (Sintra), Cantanhede, Carnaxide, Coimbra, Covilhã, Curral das Freiras, Évora, Faro, Fátima, Fundão, Ginetes, Guimarães, Lagoa (Algarve), Lagos (Algarve), Lisboa, Moscavide, Odivelas, Ovar, Ponta Delgada, Portas do Mar, Portimão, Porto, Sabadim, Salvaterra de Magos, Santarém, Seixal (Setúbal), Silves, Valbom, Vila d'Este, Vila do Conde), Spain (Granollers), UK (London) and the USA (Ann Arbor MI, Ypsilanti MI, Ripton VT).
One of the largest Hex tourneys is organized by the International Committee of Mathematical Games in Paris, France, which is annually held since 2013.
