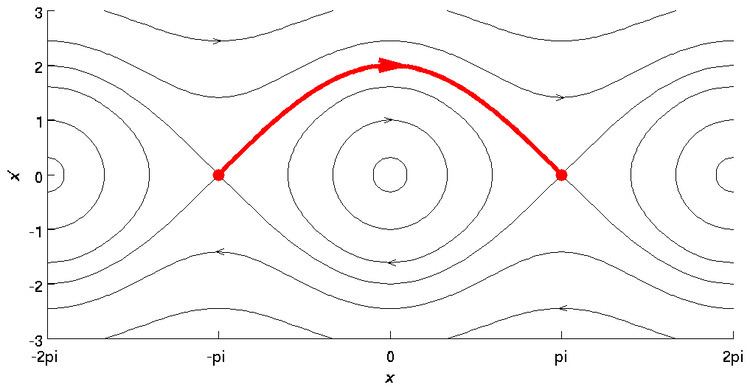
Heteroclinic orbit - Alchetron, The Free Social Encyclopedia

In mathematics, in the phase portrait of a dynamical system, a heteroclinic orbit (sometimes called a heteroclinic connection) is a path in phase space which joins two different equilibrium points. If the equilibrium points at the start and end of the orbit are the same, the orbit is a homoclinic orbit.

Consider the continuous dynamical system described by the ODE

Suppose there are equilibria at x = x 0 and x = x 1 , then a solution ϕ ( t ) is a heteroclinic orbit from x 0 to x 1 if

and

This implies that the orbit is contained in the stable manifold of x 1 and the unstable manifold of x 0 .

Symbolic dynamics

By using the Markov partition, the long-time behaviour of hyperbolic system can be studied using the techniques of symbolic dynamics. In this case, a heteroclinic orbit has a particularly simple and clear representation. Suppose that S = { 1 , 2 , … , M } is a finite set of M symbols. The dynamics of a point x is then represented by a bi-infinite string of symbols

σ = { ( … , s − 1 , s 0 , s 1 , … ) : s k ∈ S ∀ k ∈ Z }

A periodic point of the system is simply a recurring sequence of letters. A heteroclinic orbit is then the joining of two distinct periodic orbits. It may be written as

p ω s 1 s 2 ⋯ s n q ω

where p = t 1 t 2 ⋯ t k is a sequence of symbols of length k, (of course, t i ∈ S ), and q = r 1 r 2 ⋯ r m is another sequence of symbols, of length m (likewise, r i ∈ S ). The notation p ω simply denotes the repetition of p an infinite number of times. Thus, a heteroclinic orbit can be understood as the transition from one periodic orbit to another. By contrast, a homoclinic orbit can be written as

p ω s 1 s 2 ⋯ s n p ω

with the intermediate sequence s 1 s 2 ⋯ s n being non-empty, and, of course, not being p, as otherwise, the orbit would simply be p ω .

References

Heteroclinic orbit Wikipedia

(Text) CC BY-SA