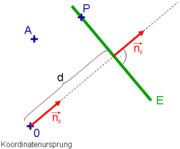
The Hesse normal form named after Otto Hesse, is an equation used in analytic geometry, and describes a line in R 2 or a plane in Euclidean space R 3 or a hyperplane in higher dimensions. It is primarily used for calculating distances (see point-plane distance and point-line distance).
It is written in vector notation as
r → ⋅ n → 0 − d = 0. The dot ⋅ indicates the scalar product or dot product. The vector n → 0 represents the unit normal vector of E or g, that points from the origin of the coordinate system to the plane (or line, in 2D). The distance d ≥ 0 is the distance from the origin to the plane (or line).
This equation is satisfied by all points P described by the location vector r → , which lie precisely in the plane E (or in 2D, on the line g).
Note: For simplicity, the following derivation discusses the 3D case. However, it is also applicable in 2D.
In the normal form,
( r → − a → ) ⋅ n → = 0 a plane is given by a normal vector n → as well as an arbitrary position vector a → of a point A ∈ E . The direction of n → is chosen to satisfy the following inequality
a → ⋅ n → ≥ 0 By dividing the normal vector n → by its magnitude | n → | , we obtain the unit (or normalized) normal vector
n → 0 = n → | n → | and the above equation can be rewritten as
( r → − a → ) ⋅ n → 0 = 0. Substituting
d = a → ⋅ n → 0 ≥ 0 we obtain the Hesse normal form
r → ⋅ n → 0 − d = 0. In this diagram, d is the distance from the origin. Because r → ⋅ n → 0 = d holds for every point in the plane, it is also true at point Q (the point where the vector from the origin meets the plane E), with r → = r → s , per the definition of the Scalar product
d = r → s ⋅ n → 0 = | r → s | ⋅ | n → 0 | ⋅ cos ( 0 ∘ ) = | r → s | ⋅ 1 = | r → s | . The magnitude | r → s | of r → s is the shortest distance from the origin to the plane.