 | ||
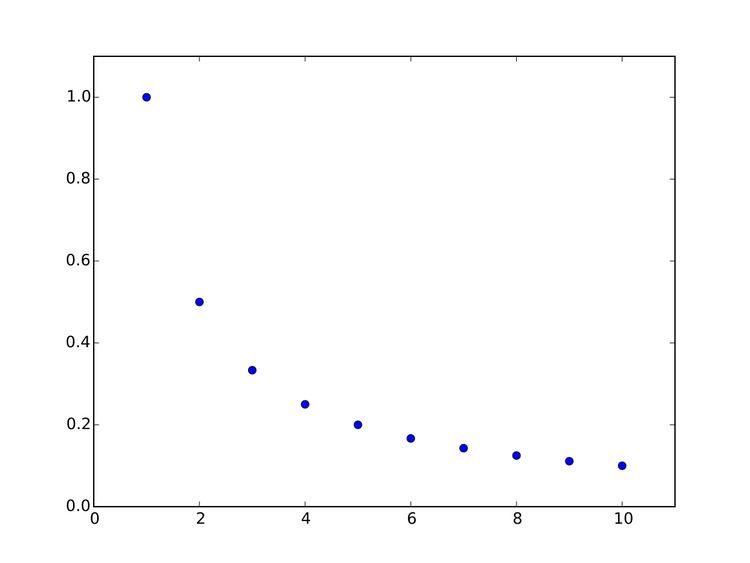
In mathematics, a harmonic progression (or harmonic sequence) is a progression formed by taking the reciprocals of an arithmetic progression. In other words, it is a sequence of the form
Contents
where −a/d is not a natural number and k is a natural number.
(Terms in the form
Equivalently, a sequence is a harmonic progression when each term is the harmonic mean of the neighboring terms.
It is not possible for a harmonic progression (other than the trivial case where a = 1 and k = 0) to sum to an integer. The reason is that, necessarily, at least one denominator of the progression will be divisible by a prime number that does not divide any other denominator.
Examples
Use in geometry
If collinear points A, B, C, and D are such that D is the harmonic conjugate of C with respect to A and B, then the distances from any one of these points to the three remaining points form harmonic progression. Specifically, each of the sequences AC, AB, AD; BC, BA, BD; CA, CD, CB; and DA, DC, DB are harmonic progressions, where each of the distances is signed according to a fixed orientation of the line.
