 | ||
Halo orbit subump
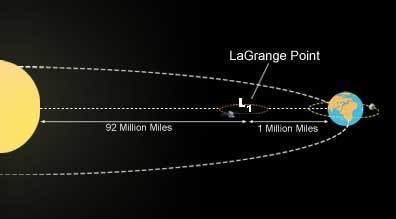
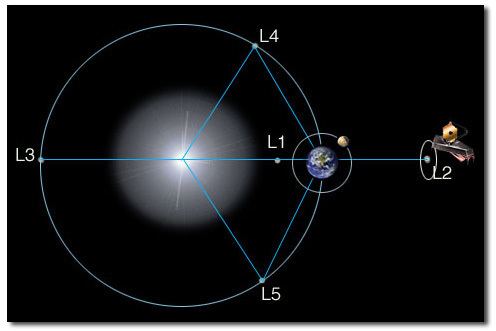
A halo orbit is a periodic, three-dimensional orbit near the L1, L2 or L3 Lagrange points in the three-body problem of orbital mechanics. Although the Lagrange point is just a point in empty space, its peculiar characteristic is that it can be orbited. Halo orbits are the result of a complicated interaction between the gravitational pull of the two planetary bodies and the Coriolis and centrifugal accelerations on a spacecraft. Halo orbits exist in any three-body system, e.g. the Sun–Earth system and the Earth–Moon system. Continuous "families" of both Northern and Southern halo orbits exist at each Lagrange point. Because halo orbits tend to be unstable, stationkeeping is required to keep a satellite on the orbit.
Contents
Halo orbit angels flight
Definition and history
Robert W. Farquhar first used the name "halo" for these orbits in his 1968 Ph.D. thesis. Farquhar advocated using spacecraft in a halo orbit on the far side of the Moon (Earth–Moon L2) as a communications relay station for an Apollo mission to the far side of the Moon. A spacecraft in such a halo orbit would be in continuous view of both the Earth and the far side of the Moon. In the end, neither a communication link satellite nor an Apollo co-mission positioned at L2 for a far side Apollo lunar landing ever took flight.
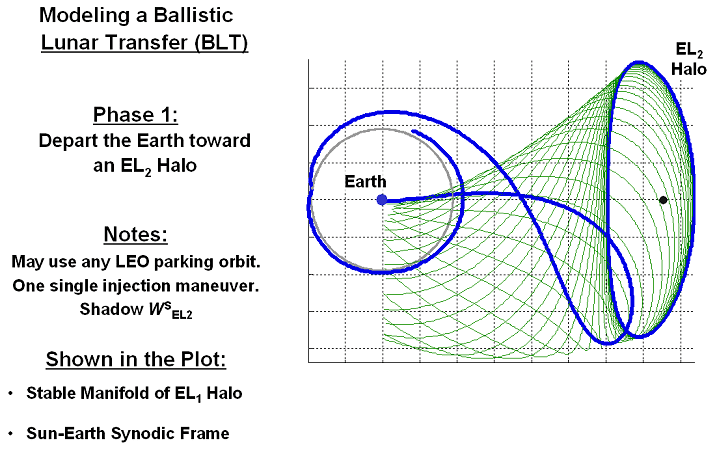
Farquhar used analytical expressions to represent halo orbits, but Kathleen Howell showed that more precise trajectories could be computed numerically.

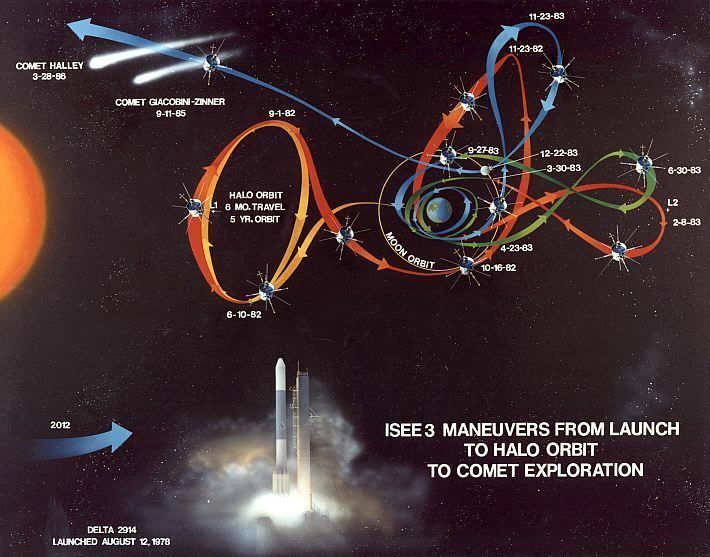
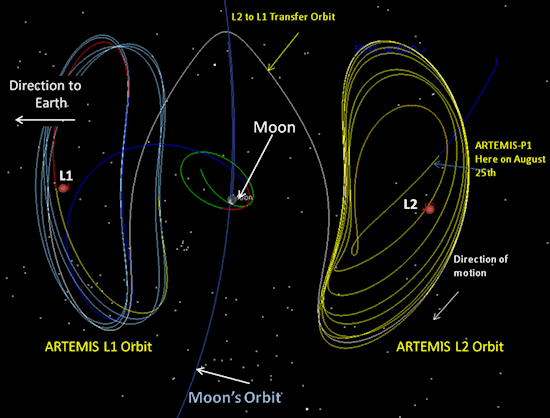
The first mission to use a halo orbit was ISEE-3, launched in 1978. It traveled to the Sun–Earth L1 point and remained there for several years. The next mission to use a halo orbit was Solar and Heliospheric Observatory (SOHO), a joint ESA and NASA mission to study the Sun, which arrived at Sun–Earth L1 in 1996. It used an orbit similar to ISEE-3. Although several other missions since then have traveled to Lagrange points, they typically have used the related non-periodic variations called Lissajous orbits than an actual halo orbit. For example, Genesis, launched in 2001, which also pioneered the use of dynamical systems theory to find low-energy transfers to and from its orbit.