Gran plot

Updated on Oct 06, 2024

Edit

Comment

A Gran plot (also known as Gran titration or the Gran method) is a common means of standardizing a titrate or titrant by estimating the equivalence volume or end point in a strong acid-strong base titration or in a potentiometric titration. Such plots have been also used to calibrate glass electrodes, to estimate the carbonate content of aqueous solutions, and to estimate the K_a values (acid dissociation constants) of weak acids and bases from titration data.

Gran plots use linear approximations of the a priori non-linear relationships between the measured quantity, pH or electromotive potential (emf), and the titrant volume. Other types of concentration measures, such as spectrophotometric absorbances or NMR chemical shifts, can in principle be similarly treated. These approximations are only valid near, but not at, the end point, and so the method differs from end point estimations by way of first- and second-derivative plots, which require data at the end point. Gran plots were originally devised for graphical determinations in pre-computer times, wherein an x-y plot on paper would be manually extrapolated to estimate the x-intercept. The graphing and visual estimation of the end point have been replaced by more accurate least-squares analyses since the advent of modern computers and enabling software packages, especially spreadsheet programs with built-in least-squares functionality.

Basis of the calculations

The Gran plot is based on the Nernst equation which can be written as

E = E 0 + s log ⁡ { H + }

where E is a measured electrode potential, E⁰ is a standard electrode potential, s is the slope, ideally equal to RT/nF, and {H⁺} is the activity of the hydrogen ion. The expression rearranges to

[ H + ] = 10 E − E 0 s o r [ H + ] = 10 − p H

depending on whether the electrode is calibrated in millivolts or pH. For convenience the concentration, [H⁺], is used in place of activity. In a titration of strong acid with strong alkali, the analytical concentration of the hydrogen ion is obtained from the initial concentration of acid, C_i and the amount of alkali added during titration.

[ H + ] = C i v i − c O H v v i + v

where v_i is the initial volume of solution, c_OH is the concentration of alkali in the burette and v is the titre volume. Equating the two expressions for [H⁺] and simplifying, the following expression is obtained

C i v i − c O H v = ( v i + v ) 10 E − E 0 s o r = ( v i + v ) 10 − p H

A plot of ( v i + v ) 10 E − E 0 s o r ( v i + v ) 10 − p H against v will be a straight line. If E⁰ and s are known from electrode calibration, where the line crosses the x-axis indicates the volume at the equivalence point, C i v i = c O H v . Alternatively, this plot can be used for electrode calibration by finding the values of E⁰ and s that give the best straight line.

Titrating strong acid with strong base

For a strong acid-strong base titration monitored by pH, we have at any i'th point in the titration

K w = [ H + ] i [ O H − ] i

where K_w is the water autoprotolysis constant.

If titrating an acid of initial volume v 0 and concentration [ H + ] 0 with base of concentration [ O H − ] 0 , then at any i'th point in the titration with titrant volume v i ,

v 0 [ H + ] 0 − v i [ O H − ] 0 v 0 + v i { ≈ [ H + ] i or 10 − p H i when v 0 [ H + ] 0 > v i [ O H − ] 0 (acidic region) = 0 when v 0 [ H + ] 0 = v i [ O H − ] 0 (equivalence point) ≈ − [ O H − ] i or − K w 10 p H i when v 0 [ H + ] 0 < v i [ O H − ] 0 (alkaline region)

At the equivalence point, the equivalence volume v e = v i .

Thus,

a plot of ( v 0 + v i ) 10 − p H i vs. v i will have a linear region before equivalence, with slope − [ O H − ] 0

and a plot of ( v 0 + v i ) 10 p H i vs. v i will have a linear region after equivalence, with slope [ O H − ] 0 / K w

both plots will have v e = v 0 [ H + ] 0 / [ O H − ] 0 as intercept

The equivalence volume is used to compute whichever of [ H + ] 0 or [ O H − ] 0 is unknown.

The pH meter is usually calibrated with buffer solutions at known pH values before starting the titration. The ionic strength can be kept constant by judicious choice of acid and base. For instance, HCl titrated with NaOH of approximately the same concentration will replace H⁺ with an ion (Na⁺) of the same charge at the same concentration, to keep the ionic strength fairly constant. Otherwise, a relatively high concentration of background electrolyte can be used, or the activity quotient can be computed.

Titrating strong base with strong acid

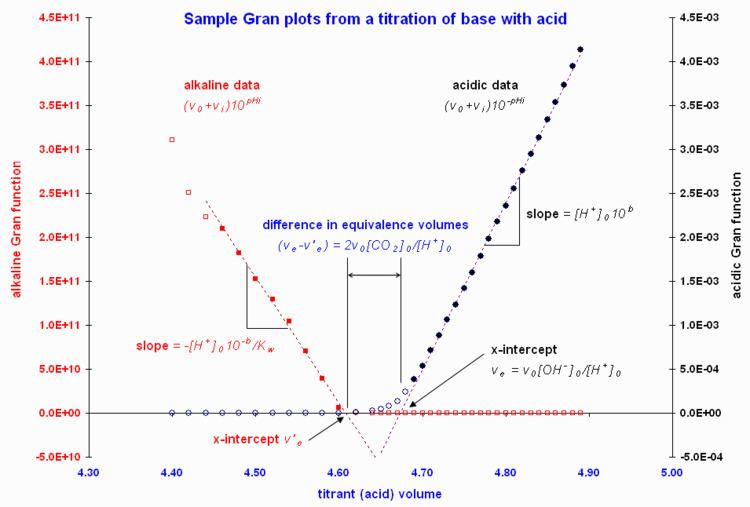
Mirror-image plots are obtained if titrating the base with the acid, and the signs of the slopes are reversed.

v 0 [ O H − ] 0 − v i [ H + ] 0 v 0 + v i { ≈ [ O H − ] i or K w 10 p H i when v 0 [ O H − ] 0 > v i [ H + ] 0 (alkaline region) = 0 when v 0 [ O H − ] 0 = v i [ H + ] 0 (equivalence point) ≈ − [ H + ] i or − 10 − p H i when v 0 [ O H − ] 0 < v i [ H + ] 0 (acidic region)

Hence,

a plot of ( v 0 + v i ) 10 p H i vs. v i will have a linear region before equivalence with slope − [ H + ] 0 / K w

and a plot of ( v 0 + v i ) 10 − p H i vs. v i will have a linear region after equivalence with slope [ H + ] 0

both plots will have v e = v 0 [ O H − ] 0 / [ H + ] 0 as x-intercept

Figure 1 gives sample Gran plots of a strong base-strong acid titration.

Concentrations and Dissociation Constants of Weak Acids

The method can be used to estimate the dissociation constants of weak acids, as well as their concentrations (Gran, 1952). With an acid represented by HA, where

K a = [ H + ] i [ A − ] i [ H A ] i ,

we have at any i'th point in the titration of a volume v 0 of acid at a concentration [ H A ] 0 by base of concentration [ O H − ] 0 . In the linear regions away from equivalence,

[ H A ] i ≈ v 0 [ H A ] 0 − v i [ O H − ] 0 v 0 + v i and [ A − ] i ≈ v i [ O H − ] 0 v 0 + v i

are valid approximations, whence

K a ≈ 10 − p H i v i [ O H − ] 0 v 0 [ H A ] 0 − v i [ O H − ] 0 , or K a ( v 0 [ H A ] 0 [ O H − ] 0 − v i ) ≈ 10 − p H i v i or, because v e = v 0 [ H A ] 0 [ O H − ] 0 , K a ( v e − v i ) ≈ 10 − p H i v i .

A plot of 10 − p H i v i versus v i will have a slope − K a over the linear acidic region and an extrapolated x-intercept v e , from which either [ H A ] 0 or [ O H − ] 0 can be computed. The alkaline region is treated in the same manner as for a titration of strong acid. Figure 2 gives an example; in this example, the two x-intercepts differ by about 0.2 mL but this is a small discrepancy, given the large equivalence volume (0.5% error).

Similar equations can be written for the titration of a weak base by strong acid (Gran, 1952; Harris, 1998).

Carbonate content

Martell and Motekaitis (1992) use the most linear regions and exploit the difference in equivalence volumes between acid-side and base-side plots during an acid-base titration to estimate the adventitious CO₂ content in the base solution. This is illustrated in the sample Gran plots of Figure 1. In that situation, the extra acid used to neutralize the carbonate, by double protonation, in volume v 0 of titrate is ( v e − v e ′ ) [ H + ] 0 = 2 v 0 [ C O 2 ] 0 . In the opposite case of a titration of acid by base, the carbonate content is similarly computed from ( v e ′ − v e ) [ O H − ] 0 = 2 v e ′ [ C O 2 ] 0 , where v e ′ is the base-side equivalence volume (from Martell and Motekaitis).

When the total CO₂ content is significant, as in natural waters and alkaline effluents, two or three inflections can be seen in the pH-volume curves owing to buffering by higher concentrations of bicarbonate and carbonate. As discussed by Stumm and Morgan (1981), the analysis of such waters can use up to six Gran plots from a single titration to estimate the multiple end points and measure the total alkalinity and the carbonate and/or bicarbonate contents.

Potentiometric monitoring of H+

To use potentiometric (e.m.f.) measurements E i in monitoring the H + concentration in place of p H i readings, one can trivially set − l o g 10 [ H + ] i = b 0 − b 1 E i and apply the same equations as above, where b 0 is the offset correction n F E 0 / R T , and b 1 is a slope correction n F / R T (1/59.2 pH units/mV at 25°C), such that − b 1 E i replaces p H i .

Thus, as before for a titration of strong acid by strong base,

a plot of ( v 0 + v i ) 10 b 1 E i vs. v i will have a linear region before equivalence, with slope − 10 b 0 [ O H − ] 0

and a plot of ( v 0 + v i ) 10 − b 1 E i vs. v i will have a linear region after equivalence, with slope 10 − b 0 [ O H − ] 0 / K w

both plots will have v e = v 0 [ H + ] 0 / [ O H − ] 0 as intercept and, as before, the acid-side equivalence volume can be used to standardize whichever concentration is unknown, and the difference between acid-side and base-side equivalence volumes can be used to estimate the carbonate content

Analogous plots can be drawn using data from a titration of base by acid.

Electrode calibration

Note that the above analysis requires prior knowledge of b 0 and b 1 .

If a pH electrode is not well calibrated, an offset correction can be computed in situ from the acid-side Gran slope:

For a titration of acid by base, the acid-side slope ( − [ O H − ] 0 10 b 0 ) can serve to compute b 0 using a known value of [ O H − ] 0 or using the value given by the equivalence volume. K w can then be computed from the base-side slope.

For a titration of base by acid, as illustrated in the sample plots, the acid-side slope ( [ H + ] 0 10 b 0 ) is similarly used to compute b 0 and the base-side slope ( − [ H + ] 0 10 − b 0 / K w ) is used to compute K w using a known value of [ H + ] 0 or using the value given by the acid-side equivalence volume.

In the sample data illustrated in Figure 1, this offset correction was not insignificant, at -0.054 pH units.

The value of b 1 , however, may deviate from its theoretical value and can only be assessed by a proper calibration of the electrode. Calibration of an electrode is often performed using buffers of known pH, or by performing a titration of strong acid with strong base. In that case, a constant ionic strength can be maintained, and [ H + ] i is known at all titration points if both [ H + ] 0 and [ O H − ] 0 are known (and should be directly related to primary standards). For instance, Martell and Motekaitis (1992) calculated the pH value expected at the start of the titration, having earlier titrated the acid and base solutions against primary standards, then adjusted the pH electrode reading accordingly, but this does not afford a slope correction if one is needed.

Based on earlier work by McBryde (1969), Gans and O'Sullivan (2000) describe an iterative approach to arrive at both b 0 and b 1 values in the relation − l o g 10 [ H + ] i = b 0 − b 1 E i , from a titration of strong acid by strong base:

The procedure could in principle be modified for titrations of base by acid. A computer program named GLEE (for GLass Electrode Evaluation) implements this approach on titrations of acid by base for electrode calibration. This program additionally can compute (by a separate, non-linear least-squares process) a 'correction' for the base concentration. An advantage of this method of electrode calibration is that it can be performed in the same medium of constant ionic strength which may later be used for the determination of equilibrium constants.
Note that the regular Gran functions will provide the required equivalence volumes and, as b 1 is initially set at its theoretical value, the initial estimate for b 0 in step 1 can be had from the slope of the regular acid-side Gran function as detailed earlier. Note too that this procedure computes the CO₂ content and can indeed be combined with a complete standardization of the base, using the definition of v e to compute [ O H − ] 0 . Finally, the usable pH range could be extended by solving the quadratic ( v 0 [ H + ] 0 − v i [ O H − ] 0 ) / ( v 0 + v i ) = [ H + ] i − K w / [ H + ] i for [ H + ] i .

Potentiometric monitoring of other species

Potentiometric data are also used to monitor species other than H + . When monitoring any species S 1 by potentiometry, one can apply the same formalism with − l o g 10 [ S 1 ] i = b 0 − b 1 E i . Thus, a titration of a solution of another species S 2 by species S 1 is analogous to a pH-monitored titration of base by acid, whence either ( v 0 + v i ) 10 b 1 E i or ( v 0 + v i ) 10 − b 1 E i plotted versus v i will have an x-intercept v 0 [ S 0 ] 0 / [ S 1 ] 0 . In the opposite titration of S 1 by S 2 , the equivalence volume will be v 0 [ S 1 ] 0 / [ S 0 ] 0 . The significance of the slopes will depend on the interactions between the two species, whether associating in solution or precipitating together (Gran, 1952). Usually, the only result of interest is the equivalence point. However, the before-equivalence slope could in principle be used to assess the solubility product K s p in the same way as K w can be determined from acid-base titrations, although other ion-pair association interactions may be occurring as well.

To illustrate, consider a titration of Cl⁻ by Ag⁺ monitored potentiometrically: v 0 [ C l − ] 0 − v i [ A g + ] 0 v 0 + v i { ≈ [ C l − ] i or K s p 10 − b 1 E i + b 0 when v 0 [ C l − ] 0 > v i [ A g + ] 0 (before equivalence) = 0 when v 0 [ C l − ] 0 = v i [ A g + ] 0 (equivalence point) ≈ − [ A g + ] i or − 10 b 1 E i − b 0 when v 0 [ C l − ] 0 < v i [ A g + ] 0 (after equivalence)

Hence,

a plot of ( v 0 + v i ) 10 − b 1 E i vs. v i will have a linear region before equivalence, with slope − [ A g + ] 0 10 − b 0 / K s p

and a plot of ( v 0 + v i ) 10 b 1 E i vs. v i will have a linear region after equivalence, with slope [ A g + ] 0 10 b 0

in both plots, the x-intercept is v e = v 0 [ C l − ] 0 / [ A g + ] 0

Figure 3 gives sample plots of potentiometric titration data.

Non-ideal behaviour

In any titration lacking buffering components, both before-equivalence and beyond-equivalence plots should ideally cross the x axis at the same point. Non-ideal behaviour can result from measurement errors (e.g. a poorly calibrated electrode, an insufficient equilibration time before recording the electrode reading, drifts in ionic strength), sampling errors (e.g. low data densities in the linear regions) or an incomplete chemical model (e.g. the presence of titratable impurities such as carbonate in the base, or incomplete precipitation in potentiometric titrations of dilute solutions, for which Gran et al. (1981) propose alternate approaches). Buffle et al. (1972) discuss a number of error sources.

Because the 10 p H i or 10 − p H i terms in the Gran functions only asymptotically tend toward, and never reach, the x axis, curvature approaching the equivalence point is to be expected in all cases. However, there is disagreement among practitioners as to which data to plot, whether using only data on one side of equivalence or on both sides, and whether to select data nearest equivalence or in the most linear portions: using the data nearest the equivalence point will enable the two x-intercepts to be more coincident with each other and to better coincide with estimates from derivative plots, while using acid-side data in an acid-base titration presumably minimizes interference from titratable (buffering) impurities, such as bicarbonate/carbonate in the base (see Carbonate content), and the effect of a drifting ionic strength. In the sample plots displayed in the Figures, the most linear regions (the data represented by filled circles) were selected for the least-squares computations of slopes and intercepts. Data selection is always subjective.

References

Gran plot Wikipedia

(Text) CC BY-SA

Contents