Golden section search

Basic idea

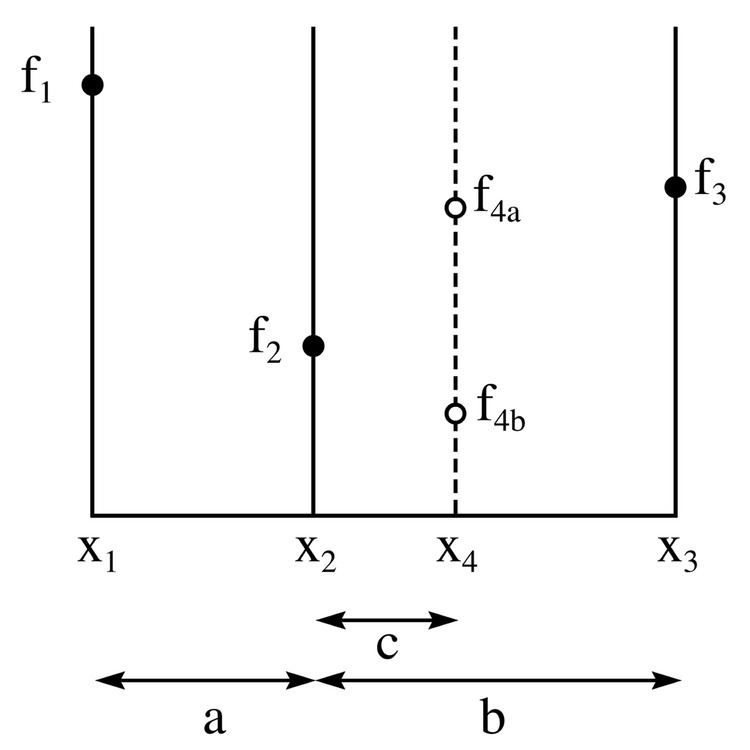
The discussion here is posed in terms of searching for a minimum (searching for a maximum is similar) of a unimodal function. Unlike finding a zero, where two function evaluations with opposite sign are sufficient to bracket a root, when searching for a minimum, three values are necessary. The golden-section search is an efficient way to reduce progressively the interval locating the minimum. The key is to observe that regardless of how many points have been evaluated, the minimum lies within the interval defined by the two points adjacent to the point with the least value so far evaluated.

The diagram above illustrates a single step in the technique for finding a minimum. The functional values of f ( x ) are on the vertical axis, and the horizontal axis is the x parameter. The value of f ( x ) has already been evaluated at the three points: x 1 , x 2 , and x 3 . Since f 2 is smaller than either f 1 or f 3 , it is clear that a minimum lies inside the interval from x 1 to x 3 .

The next step in the minimization process is to "probe" the function by evaluating it at a new value of x, namely x 4 . It is most efficient to choose x 4 somewhere inside the largest interval, i.e. between x 2 and x 3 . From the diagram, it is clear that if the function yields f 4 a , then a minimum lies between x 1 and x 4 , and the new triplet of points will be x 1 , x 2 , and x 4 . However, if the function yields the value f 4 b , then a minimum lies between x 2 and x 3 , and the new triplet of points will be x 2 , x 4 , and x 3 . Thus, in either case, we can construct a new narrower search interval that is guaranteed to contain the function's minimum.

Probe point selection

From the diagram above, it is seen that the new search interval will be either between x 1 and x 4 with a length of a + c, or between x 2 and x 3 with a length of b. The golden-section search requires that these intervals be equal. If they are not, a run of "bad luck" could lead to the wider interval being used many times, thus slowing down the rate of convergence. To ensure that b = a + c, the algorithm should choose x 4 = x 1 + ( x 3 − x 2 ) .

However, there still remains the question of where x 2 should be placed in relation to x 1 and x 3 . The golden-section search chooses the spacing between these points in such a way that these points have the same proportion of spacing as the subsequent triple x 1 , x 2 , x 4 or x 2 , x 4 , x 3 . By maintaining the same proportion of spacing throughout the algorithm, we avoid a situation in which x 2 is very close to x 1 or x 3 and guarantee that the interval width shrinks by the same constant proportion in each step.

Mathematically, to ensure that the spacing after evaluating f ( x 4 ) is proportional to the spacing prior to that evaluation, if f ( x 4 ) is f 4 a and our new triplet of points is x 1 , x 2 , and x 4 , then we want

However, if f ( x 4 ) is f 4 b and our new triplet of points is x 2 , x 4 , and x 3 , then we want

Eliminating c from these two simultaneous equations yields

or

where φ is the golden ratio:

The appearance of the golden ratio in the proportional spacing of the evaluation points is how this search algorithm gets its name.

Termination condition

Because smooth functions are flat (their first derivative is close to zero) near a minimum, attention must be paid not to expect too great an accuracy in locating the minimum. The termination condition provided in the book Numerical Recipes in C is based on testing the gaps among x 1 , x 2 , x 3 and x 4 , terminating when within the relative accuracy bounds

where τ is a tolerance parameter of the algorithm, and | x | is the absolute value of x . The check is based on the bracket size relative to its central value, because that relative error in x is approximately proportional to the squared absolute error in f ( x ) in typical cases. For that same reason, the Numerical Recipes text recommends that τ = ε , where ε is the required absolute precision of f ( x ) .

Iterative algorithm

Recursive algorithm

To realise the advantage of golden section search, the function f ( x ) would be implemented with caching, so that in all invocations of goldenSectionSearch(..) above, except the first, f ( x 2 ) would have already been evaluated previously — the result of the calculation will be re-used, bypassing the (perhaps expensive) explicit evaluation of the function. Together with a slightly smaller number of recursions, this 50% saving in the number of calls to f ( x ) is the main algorithmic advantage over Ternary search.

Fibonacci search

A very similar algorithm can also be used to find the extremum (minimum or maximum) of a sequence of values that has a single local minimum or local maximum. In order to approximate the probe positions of golden section search while probing only integer sequence indices, the variant of the algorithm for this case typically maintains a bracketing of the solution in which the length of the bracketed interval is a Fibonacci number. For this reason, the sequence variant of golden section search is often called Fibonacci search.

Fibonacci search was first devised by Kiefer (1953) as a minimax search for the maximum (minimum) of a unimodal function in an interval.