Glossary of module theory

Basic definition

left R-module

A left module M over the ring R is an abelian group ( M , + ) with an operation R × M → M (called scalar multipliction) satisfies the following condition: ∀ r , s ∈ R , m , n ∈ M ,

1. r ( m + n ) = r m + r n
2. r ( s m ) = ( r s ) m
3. 1 R m = m

right R-module

A right module M over the ring R is an abelian group ( M , + ) with an operation M × R → M satisfies the following condition: ∀ r , s ∈ R , m , n ∈ M ,

1. ( m + n ) r = m r + n r
2. ( m s ) r = r ( s m )
3. m 1 R = m

Or it can be defined as the left module M over R op (the opposite ring of R ).

bimodule

If an abelian group M is both a left S -module and right R -module, it can be made to a ( S , R ) -bimodule if s ( m r ) = ( s m ) r ∀ s ∈ S , r ∈ R , m ∈ M .

submodule

Given M is a left R -module, a subgroup N of M is a submodule if R N ⊆ N .

homomorphism of R -modules

For two left R -modules M 1 , M 2 , a group homomorphism ϕ : M 1 → M 2 is called homomorphism of R -modules if r ϕ ( m ) = ϕ ( r m ) ∀ r ∈ R , m ∈ M 1 .

quotient module

Given a left R -modules M , a submodule N , M / N can be made to a left R -module by r ( m + N ) = r m + N ∀ r ∈ R , m ∈ M . It is also called a factor module.

annihilator

The annihilator of a left R -module M is the set Ann ( M ) := { r ∈ R | r m = 0 ∀ m ∈ M } . It is a (left) ideal of R . The annihilator of an element m ∈ M is the set Ann ( m ) := { r ∈ R | r m = 0 } .

Types of modules

finitely generated module

A module M is finitely generated if there exist finitely many elements x 1 , . . . , x n in M such that every element of M is a finite linear combination of those elements with coefficients from the scalar ring R .

cyclic module

A module is called a cyclic module if it is generated by one element.

free module

A free module is a module that has a basis, or equivalently, one that is isomorphic to a direct sum of copies of the scalar ring R .

basis

A basis of a module M is a set of elements in M such that every element in the module can be expressed as a finite sum of elements in the basis in a unique way.

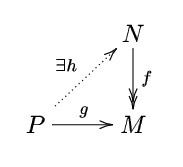
Projective module

A R -module P is called a projective module if given a R -module homomorphism g : P → M , and a surjective R -module homomorphism f : N → M , there exists a R -module homomorphism h : P → N such that f ∘ h = g .

The covariant functor Hom R ( P , − ) is exact.

M is a projective module.

Every short exact sequence 0 → L → L ′ → P → 0 is split.

M is a direct summand of free modules.

In particular, every free module is projective.

injective module

A R -module Q is called an injective module if given a R -module homomorphism g : X → Q , and an injective R -module homomorphism f : X → Y , there exists a

R -module homomorphism h : Y → Q such that f ∘ h = g .

The contravariant functor Hom R ( − , I ) is exact.

I is a injective module.

Every short exact sequence 0 → I → L → L ′ → 0 is split.

flat module

A R -module F is called a flat module if the tensor product functor − ⊗ R F is exact. In particular, every projective module is flat.

simple module

A simple module is a nonzero module whose only submodules are zero and itself.

indecomposable module

An indecomposable module is a non-zero module that cannot be written as a direct sum of two non-zero submodules. Every simple module is indecomposable.

principal indecomposable module

A cyclic indecomposable projective module is known as a PIM.

semisimple module

A module is called semisimple if it is the direct sum of simple submodules.

faithful module

A faithful module M is one where the action of each nonzero r ∈ R on M is nontrivial (i.e. r x ≠ 0 for some x in M). Equivalently, Ann ( M ) is the zero ideal.

Noetherian module

A Noetherian module is a module such that every submodule is finitely generated. Equivalently, every increasing chain of submodules becomes stationary after finitely many steps.

Artinian module

An Artinian module is a module in which every decreasing chain of submodules becomes stationary after finitely many steps.

finite length module

A module which is both Artinian and Noetherian has additional special properties.

graded module

A module M over a graded ring A = ⨁ n ∈ N A n is a graded module if M can be expressed as a direct sum ⨁ i ∈ N M i and A i M j ⊆ M i + j .

invertible module

Roughly synonymous to rank 1 projective module.

uniform module

Module in which every two non-zero submodules have a non-zero intersection.

algebraically compact module (pure injective module)

Modules in which all systems of equations can be decided by finitary means. Alternatively, those modules which leave pure-exact sequence exact after applying Hom.

injective cogenerator

An injective module such that every module has a nonzero homomorphism into it.

irreducible module

synonymous to "simple module"

completely reducible module

synonymous to "semisimple module"

Operations on modules

Direct sum of modules

Tensor product of modules

Hom functor

Ext functor

Tor functor

Essential extension

An extension in which every nonzero submodule of the larger module meets the smaller module in a nonzero submodule.

Injective envelope

A maximal essential extension, or a minimal embedding in an injective module

Projective cover

A minimal surjection from a projective module.

Socle

The largest semisimple submodule

Radical of a module

The intersection of the maximal submodules. For Artinian modules, the smallest submodule with semisimple quotient.

Changing scalars

Restriction of scalars

Uses a ring homomorphism from R to S to convert S-modules to R-modules

Extension of scalars

Uses a ring homomorphism from R to S to convert R-modules to S-modules

Localization of a module

Converts R modules to S modules, where S is a localization of R

Endomorphism ring

A left R-module is a right S-module where S is its endomorphism ring.

Homological algebra

Mittag-Leffler condition (ML)

Short five lemma

Five lemma

Snake lemma

Modules over special rings

D-module

A module over a ring of differential operators.

Drinfeld module

A module over a ring of functions on algebraic curve with coefficients from a finite field.

Galois module

A module over the group ring of a Galois group

Structure theorem for finitely generated modules over a principal ideal domain

Finitely generated modules over PIDs are finite direct sums of primary cyclic modules.

Tate module

A special kind of Galois module

Miscellaneous

Rational canonical form

elementary divisor

invariants

fitting ideal

normal forms for matrices

Jordan Hölder composition series

tensor product