Gershgorin circle theorem

Statement and proof

Let A be a complex n × n matrix, with entries a i j . For i ∈ { 1 , … , n } let R i = ∑ j ≠ i | a i j | be the sum of the absolute values of the non-diagonal entries in the i -th row. Let D ( a i i , R i ) be the closed disc centered at a i i with radius R i . Such a disc is called a Gershgorin disc.

Theorem: Every eigenvalue of A lies within at least one of the Gershgorin discs D ( a i i , R i )

Proof: Let λ be an eigenvalue of A and let x = (x_j) be a corresponding eigenvector. Let i ∈ {1, …, n} be chosen so that |x_i| = max_j |x_j|. (That is to say, choose i so that x_i is the largest (in absolute value) number in the vector x) Then |x_i| > 0, otherwise x = 0. Since x is an eigenvector, A x = λ x , and thus:

So, splitting the sum, we get

We may then divide both sides by x_i (choosing i as we explained, we can be sure that x_i ≠ 0) and take the absolute value to obtain

where the last inequality is valid because

Corollary: The eigenvalues of A must also lie within the Gershgorin discs C_j corresponding to the columns of A.

Proof: Apply the Theorem to A^T.

Example For a diagonal matrix, the Gershgorin discs coincide with the spectrum. Conversely, if the Gershgorin discs coincide with the spectrum, the matrix is diagonal.

Discussion

One way to interpret this theorem is that if the off-diagonal entries of a square matrix over the complex numbers have small norms, the eigenvalues of the matrix cannot be "far from" the diagonal entries of the matrix. Therefore, by reducing the norms of off-diagonal entries one can attempt to approximate the eigenvalues of the matrix. Of course, diagonal entries may change in the process of minimizing off-diagonal entries.

Strengthening of the theorem

If one of the discs is disjoint from the others then it contains exactly one eigenvalue. If however it meets another disc it is possible that it contains no eigenvalue (for example, A = ( 0 1 4 0 ) or A = ( 1 − 2 1 − 1 ) ). In the general case the theorem can be strengthened as follows:

Theorem: If the union of k discs is disjoint from the union of the other n − k discs then the former union contains exactly k and the latter n − k eigenvalues of A.

Proof: Let D be the diagonal matrix with entries equal to the diagonal entries of A and let

We will use the fact that the eigenvalues are continuous in t , and show that if any eigenvalue moves from one of the unions to the other, then it must be outside all the discs for some t , which is a contradiction.

The statement is true for D = B ( 0 ) . The diagonal entries of B ( t ) are equal to that of A, thus the centers of the Gershgorin circles are the same, however their radii are t times that of A. Therefore the union of the corresponding k discs of B ( t ) is disjoint from the union of the remaining n-k for all t ∈ [ 0 , 1 ] . The discs are closed, so the distance of the two unions for A is d > 0 . The distance for B ( t ) is a decreasing function of t, so it is always at least d. Since the eigenvalues of B ( t ) are a continuous function of t, for any eigenvalue λ ( t ) of B ( t ) in the union of the k discs its distance d ( t ) from the union of the other n-k discs is also continuous. Obviously d ( 0 ) ≥ d , and assume λ ( 1 ) lies in the union of the n-k discs. Then d ( 1 ) = 0 , so there exists 0 < t 0 < 1 such that 0 < d ( t 0 ) < d . But this means λ ( t 0 ) lies outside the Gershgorin discs, which is impossible. Therefore λ ( 1 ) lies in the union of the k discs, and the theorem is proven.

Application

The Gershgorin circle theorem is useful in solving matrix equations of the form Ax = b for x where b is a vector and A is a matrix with a large condition number.

In this kind of problem, the error in the final result is usually of the same order of magnitude as the error in the initial data multiplied by the condition number of A. For instance, if b is known to six decimal places and the condition number of A is 1000 then we can only be confident that x is accurate to three decimal places. For very high condition numbers, even very small errors due to rounding can be magnified to such an extent that the result is meaningless.

It would be good to reduce the condition number of A. This can be done by preconditioning: A matrix P such that P ≈ A⁻¹ is constructed, and then the equation PAx = Pb is solved for x. Using the exact inverse of A would be nice but finding the inverse of a matrix is generally very difficult.

Now, since PA ≈ I where I is the identity matrix, the eigenvalues of PA should all be close to 1. By the Gershgorin circle theorem, every eigenvalue of PA lies within a known area and so we can form a rough estimate of how good our choice of P was.

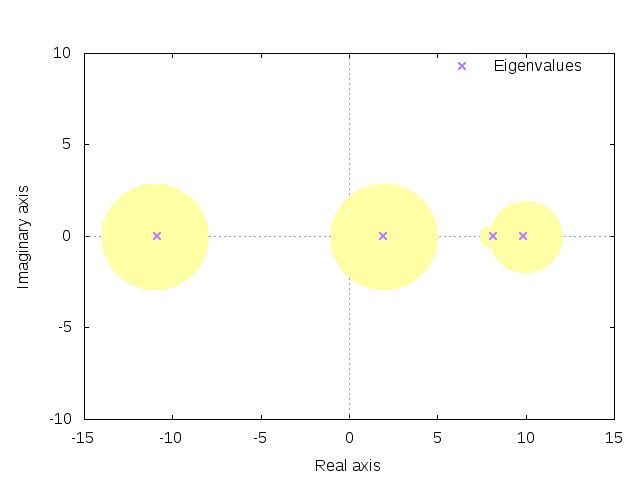
Example

Use the Gershgorin circle theorem to estimate the eigenvalues of:

Starting with row one, we take the element on the diagonal, a_ii as the center for the disc. We then take the remaining elements in the row and apply the formula:

to obtain the following four discs:

Note that we can improve the accuracy of the last two discs by applying the formula to the corresponding columns of the matrix, obtaining D ( 2 , 1.2 ) and D ( − 11 , 2.2 ) .

The eigenvalues are 9.8218, 8.1478, 1.8995, -10.86