Rahul Sharma (Editor)

Garnir relations

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Garnir relations

In mathematics, the Garnir relations give a way of expressing a basis of the Specht modules Vλ in terms of standard polytabloids.

Contents

Specht modules in terms of polytabloids

Given a partition λ of n, one has the Specht module Vλ. In characteristic 0, this is an irreducible representation of the symmetric group Sn. One can construct Vλ explicitly in terms of polytabloids as follows:

  • Start with the permutation representation of Sn acting on all Young tableaux of shape λ, where Sn acts by permuting the entries in each tableau. Note that we do not require the tableaux to be standard.
  • Extend this to an action of Sn on all (row) Young tabloids, which are orbits of Young tableaux under the action of the Young row subgroups (two Young tableaux of shape λ, where λ = λ 1 + ⋯ + λ r , are equivalent if they are in the same orbit of S λ 1 × ⋯ × S λ r ⩽ S n , acting by permuting the entries in each row).
  • Now consider polytabloids, these are formal linear combinations of Young tabloids, with integer coefficients. Given any Young tableau T, one defines the associated polytabloid by acting on T with the Young column subgroup S μ 1 × ⋯ × S μ s , where μ = μ 1 + ⋯ + μ s is the conjugate partition to λ. One writes a polytabloid S = T σ corresponding to each element in this orbit, affected with the sign of the permutation σ taking T to S. One then writes eT for the corresponding polytabloid:
    • e T = ∑ σ ∈ S μ 1 × ⋯ × S μ s sgn ⁡ ( σ ) T σ .
  • The Specht module Vλ is then the subspace of the space of all polytabloids spanned by the polytabloids obtained from Young tableaux in the above fashion.

    • Straightening polytabloids and the Garnir elements

    The above construction gives an explicit description of the Specht module Vλ. However, the polytabloids associated to different Young tableaux are not necessarily linearly independent, indeed one expects the dimension of Vλ to be exactly the number of standard Young tableaux of shape λ. In fact, the polytabloids associated to standard Young tableaux span Vλ; to express other polytabloids in terms of them, one uses a straightening algorithm.

    Given a Young tableau S, we construct the polytabloid eS as above. Without loss of generality, all columns of S are increasing, otherwise we could instead start with the modified Young tableau with increasing columns, whose polytabloid will differ at most by a sign. S is then said to not have any column descents. We want to express eS as a linear combination of standard polytabloids, i.e. polytabloids associated to standard Young tableaux. To do this, we would like permutations πi such that in all tableaux Sπi, a row descent has been eliminated, with S ( 1 + ∑ i π i ) = 0 . This then expresses S in terms of polytabloids that are closer to being standard. The permutations that achieve this are the Garnir elements.

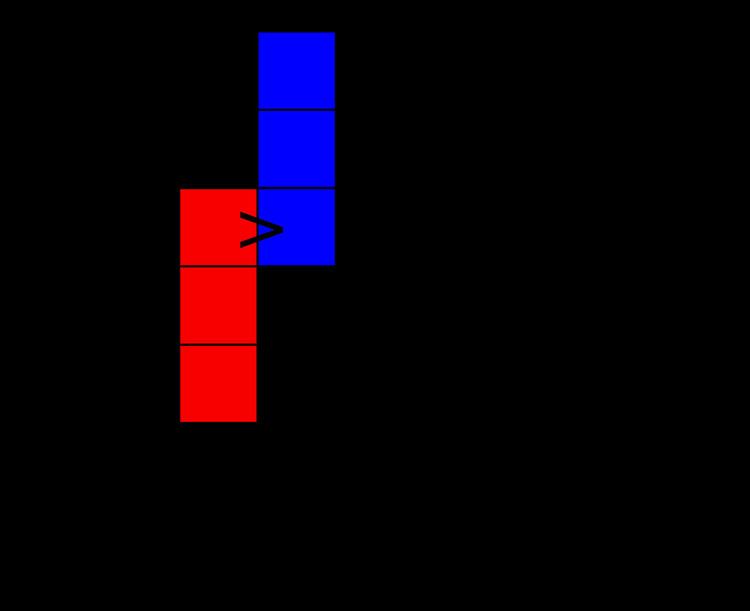
    Suppose we want to eliminate a row descent in the Young tableau T. We pick two subsets A and B of the boxes of T as in the following diagram:

    Then the Garnir element g A , B is defined to be ∑ i sgn ⁡ ( π i ) π i , where the πi are the permutations of the entries of the boxes of A and B that keep both subsets A and B without column descents.

    Example

    Consider the following Young tableau:

    There is a row descent in the second row, so we choose the subsets A and B as indicated, which gives us the following:

    This gives us the Garnir element g A , B = 1 − ( 45 ) + ( 245 ) + ( 465 ) − ( 2465 ) + ( 25 ) ( 46 ) . This allows us to remove the row descent in the second row, but this has also introduced other descents in other places. But there is a way in which all tableaux obtained like this are closer to being standard, this is measured by a dominance order on polytabloids. Therefore, one can repeatedly apply this procedure to straighten a polytabloid, eventually writing it as a linear combination of standard polytabloids, showing that the Specht module is spanned by the standard polytabloids. As they are also linearly independent, they form a basis of this module.

    Other interpretations

    There is a similar description for the irreducible representations of GLn. In that case, one can consider the Weyl modules associated to a partition λ, which can be described in terms of bideterminants. One has a similar straightening algorithm, but this time in terms of semistandard Young tableaux.

    References

    Garnir relations Wikipedia
    (Text) CC BY-SA