 | ||
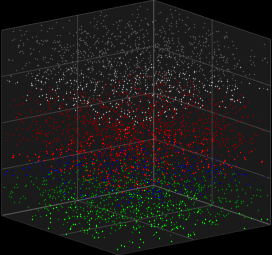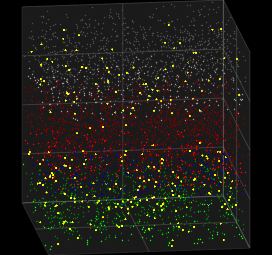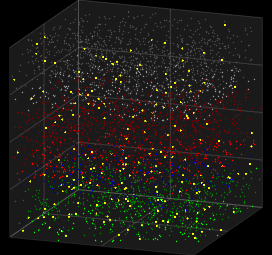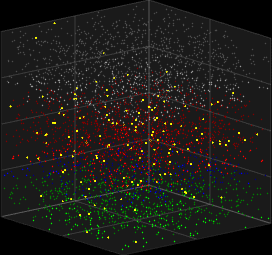
The Galves–Löcherbach model is a model with intrinsic stochasticity for biological neural nets, in which the probability of a future spike depends on the evolution of the complete system since the last spike. This model of spiking neurons was developed by mathematicians Antonio Galves and Eva Löcherbach. In the first article on the model, in 2013, they called it a model of a "system with interacting stochastic chains with memory of variable length."
Contents
History
Some inspirations of the Galves–Löcherbach model are the Frank Spitzer's interacting particle system and Jorma Rissanen's notion of stochastic chain with memory of variable length. Another work that influenced this model was Bruno Cessac's study on the leaky integrate-and-fire model, who himself was influenced by Hédi Soula. Galves and Löcherbach referred to the process that Cessac described as "a version in a finite dimension" of their own probabilistic model.
Prior integrate-and-fire models with stochastic characteristics relied on including a noise to simulate stochasticity. The Galves–Löcherbach model distinguishes itself because it is inherently stochastic, incorporating probabilistic measures directly in the calculation of spikes. It is also a model that may be applied relatively easily, from a computational standpoint, with a good ratio between cost and efficiency. It remains a non-Markovian model, since the probability of a given neuronal spike depends on the accumulated activity of the system since the last spike.
Contributions to the model were made, considering the hydrodynamic limit of the interacting neuronal system, the long-range behavior and aspects pertaining to the process in the sense of predicting and classifying behaviors according to a fonction of parameters, and the generalization of the model to the continuous time.
The Galves–Löcherbach model was a cornerstone to the Research, Innocation and Dissemination Center for Neuromathematics.
Formal definition
The model considers a countable set of neurons
Furthermore, the probability that a given neuron
where
At time
