Gabor wavelet - Alchetron, The Free Social Encyclopedia

Gabor wavelets are wavelets invented by Dennis Gabor using complex functions constructed to serve as a basis for Fourier transforms in information theory applications. They are very similar to Morlet wavelets. They are also closely related to Gabor filters (see Gabor filter#Wavelet space). The important property of the wavelet is that it minimizes the product of its standard deviations in the time and frequency domain. Put another way, the uncertainty in information carried by this wavelet is minimized. However they have the downside of being non-orthogonal, so efficient decomposition into the basis is difficult. Since their inception, various applications have appeared, from image processing to analyzing neurons in the human visual system.

Minimal uncertainty property

The motivation for Gabor wavelets comes from finding some function f ( x ) which minimizes its standard deviation in the time and frequency domains. More formally, the variance in the position domain is:

( Δ x ) 2 = ∫ − ∞ ∞ ( x − μ ) 2 f ( x ) f ∗ ( x ) d x ∫ − ∞ ∞ f ( x ) f ∗ ( x ) d x

where f ∗ ( x ) is the complex conjugate of f ( x ) and μ is the arithmetic mean, defined as:

μ = ∫ − ∞ ∞ x f ( x ) f ∗ ( x ) d x ∫ − ∞ ∞ f ( x ) f ∗ ( x ) d x

The variance in the wave number domain is:

( Δ k ) 2 = ∫ − ∞ ∞ ( k − k 0 ) 2 F ( k ) F ∗ ( k ) d k ∫ − ∞ ∞ F ( k ) F ∗ ( k ) d k

Where k 0 is the arithmetic mean of the Fourier Transform of f ( x ) , F ( x ) :

k 0 = ∫ − ∞ ∞ k F ( k ) F ∗ ( k ) d k ∫ − ∞ ∞ F ( k ) F ∗ ( k ) d k

With these defined, the uncertainty is written as:

( Δ x ) ( Δ k )

This quantity has been shown to have a lower bound of 1 2 . The quantum mechanics view is to interpret ( Δ x ) as the uncertainty in position and ℏ ( Δ k ) as uncertainty in momentum. A function f ( x ) that has the lowest theoretically possible uncertainty bound is the Gabor Wavelet.

Equation

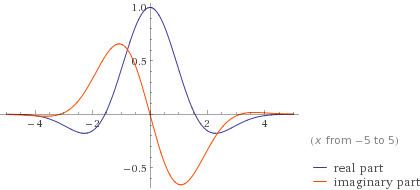
The equation of a 1-D Gabor wavelet is a Gaussian modulated by a complex exponential, described as follows:

f ( x ) = e − ( x − x 0 ) 2 / a 2 e − i k 0 ( x − x 0 )

As opposed to other functions commonly used as bases in Fourier Transforms such as sin and cos , Gabor wavelets have locality properties, meaning that as the distance from the center x 0 increases, the value of the function becomes exponentially suppressed. a controls the rate of this exponential drop-off and k 0 controls the rate of modulation.

It is also worth noting the Fourier transform of a Gabor wavelet, which is also a Gabor wavelet:

F ( k ) = e − ( k − k 0 ) 2 a 2 e − i x 0 ( k − k 0 )

An example wavelet is given here:

References

Gabor wavelet Wikipedia

(Text) CC BY-SA

Contents

Minimal uncertainty property

Equation

References