Free energy principle

Background

The notion that self-organising biological systems – like a cell or brain – can be understood as minimising variational free energy is based upon Helmholtz’s observations on unconscious inference and subsequent treatments in psychology and machine learning. Variational free energy is a function of some outcomes and a probability density over their (hidden) causes. This variational density is defined in relation to a probabilistic model that generates outcomes from causes. In this setting, free energy provides an (upper bound) approximation to Bayesian model evidence. Its minimisation can therefore be used to explain Bayesian inference and learning. When a system actively samples outcomes to minimise free energy, it implicitly performs active inference and maximises the evidence for its (generative) model.

However, free energy is also an upper bound on the self-information (or surprise) of outcomes, where the long-term average of surprise is entropy. This means that if a system acts to minimise free energy, it will implicitly place an upper bound on the entropy of the outcomes – or sensory states – it samples.

Relationship to other theories

Active inference is closely related to the good regulator theorem and related accounts of self-organisation, such as self-assembly, pattern formation and autopoiesis. It addresses the themes considered in cybernetics, synergetics and embodied cognition. Because free energy can be expressed as the expected energy (of outcomes) under the variational density minus its entropy, it is also related to the maximum entropy principle. Finally, because the time average of energy is action, the principle of minimum variational free energy is a principle of least action.

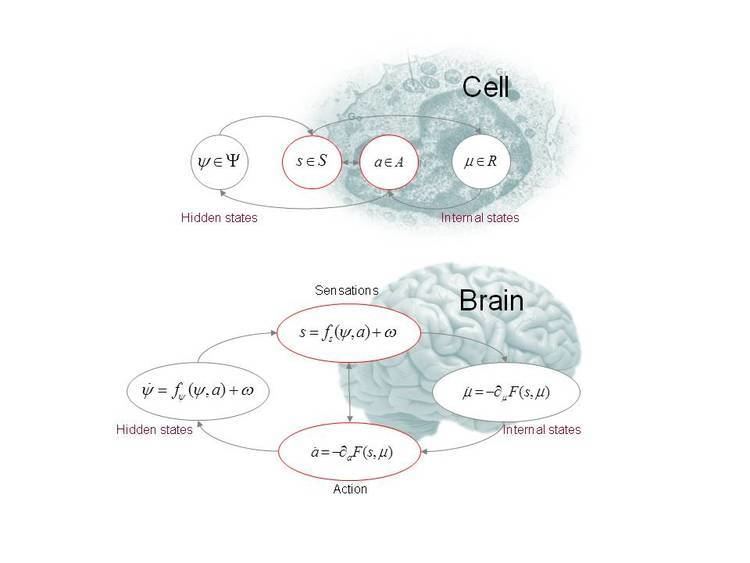
Definition

Definition (continuous formulation): Active inference rests on the tuple ( Ω , Ψ , S , A , R , q , p ) ,

Action and perception

The objective is to maximise model evidence p ( s | m ) or minimise surprise − log ⁡ p ( s | m ) . This generally involves an intractable marginalisation over hidden states, so surprise is replaced with an upper variational free energy bound. However, this means that internal states must also minimise free energy, because free energy is a functional of sensory and internal states:

This induces a dual minimisation with respect to action and internal states that correspond to action and perception respectively.

Free energy minimisation and self-organisation

Free energy minimisation has been proposed as a hallmark of self-organising systems, when cast as random dynamical systems. This formulation rests on a Markov blanket (comprising action and sensory states) that separates internal and external states. If internal states and action minimise free energy, then they place an upper bound on the entropy of sensory states

lim T → ∞ 1 T ∫ 0 T F ( s ( t ) , μ ( t ) ) d t ⏟ f r e e − a c t i o n ≥ lim T → ∞ 1 T ∫ 0 T − log ⁡ p ( s ( t ) | m ) ⏟ s u r p r i s e d t = H [ p ( s | m ) ]

This is because – under ergodic assumptions – the long-term average of surprise is entropy. This bound resists a natural tendency to disorder – of the sort associated with the second law of thermodynamics and the fluctuation theorem.

Free energy minimisation and Bayesian inference

All Bayesian inference can be cast in terms of free energy minimisation; e.g.,. When free energy is minimised with respect to internal states, the Kullback–Leibler divergence between the variational and posterior density over hidden states is minimised. This corresponds to approximate Bayesian inference – when the form of the variational density is fixed – and exact Bayesian inference otherwise. Free energy minimisation therefore provides a generic description of Bayesian inference and filtering (e.g., Kalman filtering). It is also used in Bayesian model selection, where free energy can be usefully decomposed into complexity and accuracy:

Models with minimum free energy provide an accurate explanation of data, under complexity costs (c.f., Occam's razor and more formal treatments of computational costs ). Here, complexity is the divergence between the variational density and prior beliefs about hidden states (i.e., the effective degrees of freedom used to explain the data).

Free energy minimisation and thermodynamics

Variational free energy is an information theoretic functional and is distinct from thermodynamic (Helmholtz) free energy. However, the complexity term of variational free energy shares the same fixed point as Helmholtz free energy (under the assumption the system is thermodynamically closed but not isolated). This is because if sensory perturbations are suspended (for a suitably long period of time), complexity is minimised (because accuracy can be neglected). At this point, the system is at equilibrium and internal states minimise Helmholtz free energy, by the principle of minimum energy.

Free energy minimisation and information theory

Free energy minimisation is equivalent to maximising the mutual information between sensory states and internal states that parameterise the variational density (for a fixed entropy variational density). This relates free energy minimization to the principle of minimum redundancy and related treatments using information theory to describe optimal behaviour.

Free energy minimisation in neuroscience

Free energy minimisation provides a useful way to formulate normative (Bayes optimal) models of neuronal inference and learning under uncertainty and therefore subscribes to the Bayesian brain hypothesis. The neuronal processes described by free energy minimisation depend on the nature of hidden states: Ψ = X × Θ × Π that can comprise time dependent variables, time invariant parameters and the precision (inverse variance or temperature) of random fluctuations. Minimising variables, parameters and precision corresponds to inference, learning and the encoding of uncertainty, respectively:

Perceptual inference and categorisation

Free energy minimisation formalises the notion of unconscious inference in perception and provides a normative (Bayesian) theory of neuronal processing. The associated process theory of neuronal dynamics is based on minimising free energy through gradient descent. This corresponds to generalised Bayesian filtering (where ~ denotes a variable in generalised coordinates of motion and D is a derivative matrix operator):

Usually, the generative models that define free energy are non-linear and hierarchical (like cortical hierarchies in the brain). Special cases of generalised filtering include Kalman filtering, which is formally equivalent to predictive coding – a popular metaphor for message passing in the brain. Under hierarchical models, predictive coding involves the recurrent exchange of ascending (bottom-up) prediction errors and descending (top-down) predictions that is consistent with the anatomy and physiology of sensory and motor systems.

Perceptual learning and memory

In predictive coding, optimising model parameters through a gradient ascent on the time integral of free energy (free action) reduces to associative or Hebbian plasticity and is associated with synaptic plasticity in the brain.

Perceptual precision, attention and salience

Optimising the precision parameters corresponds to optimising the gain of prediction errors (c.f., Kalman gain). In neuronally plausible implementations of predictive coding, this corresponds to optimising the excitability superficial pyramidal cells and has been interpreted in terms of attentional gain.

Active inference

When gradient descent is applied to action a ˙ = − ∂ a F ( s , μ ~ ) , motor control can be understood in terms of classical reflex arcs that are engaged by descending (corticospinal) predictions. This provides a formalism that generalizes the equilibrium point solution – to the degrees of freedom problem – to movement trajectories.

Active inference and optimal control

Active inference is related to optimal control by replacing value or cost-to-go functions with prior beliefs about state transitions or flow. This exploits the close connection between Bayesian filtering and the solution to the Bellman equation. However, active inference starts with (priors over) flow f = Γ ⋅ ∇ V + ∇ × W that are specified with scalar V ( x ) and vector W ( x ) value functions of state space (c.f., the Helmholtz decomposition). Here, Γ is the amplitude of random fluctuations and cost is c ( x ) = f ⋅ ∇ V + ∇ ⋅ Γ ⋅ V . The priors over flow p ( x ~ | m ) induce a prior over states p ( x | m ) = exp ⁡ ( V ( x ) ) that is the solution to the appropriate forward Kolmogorov equations. In contrast, optimal control optimises the flow, given a cost function, under the assumption that W = 0 (i.e., the flow is curl free or has detailed balance). Usually, this entails solving backward Kolmogorov equations.

Active inference and optimal decision (game) theory

Optimal decision problems (usually formulated as partially observable Markov decision processes) are treated within active inference by absorbing utility functions into prior beliefs. In this setting, states that have a high utility (low cost) are states an agent expects to occupy. By equipping the generative model with hidden states that model control, policies (control sequences) that minimise variational free energy lead to high utility states.

Neurobiologically, neuromodulators like dopamine are considered to report the precision of prediction errors by modulating the gain of principal cells encoding prediction error. This is closely related to – but formally distinct from – the role of dopamine in reporting prediction errors per se and related computational accounts.

Active inference and cognitive neuroscience

Active inference has been used to address a range of issues in cognitive neuroscience, brain function and neuropsychiatry, including: action observation, mirror neurons, saccades and visual search, eye movements, sleep, illusions, attention, action selection, hysteria and psychosis.