Floyd–Warshall algorithm

History and naming

The Floyd–Warshall algorithm is an example of dynamic programming, and was published in its currently recognized form by Robert Floyd in 1962. However, it is essentially the same as algorithms previously published by Bernard Roy in 1959 and also by Stephen Warshall in 1962 for finding the transitive closure of a graph, and is closely related to Kleene's algorithm (published in 1956) for converting a deterministic finite automaton into a regular expression. The modern formulation of the algorithm as three nested for-loops was first described by Peter Ingerman, also in 1962.

The algorithm is also known as Floyd's algorithm, the Roy–Warshall algorithm, the Roy–Floyd algorithm, or the WFI algorithm.

Algorithm

The Floyd–Warshall algorithm compares all possible paths through the graph between each pair of vertices. It is able to do this with Θ ( | V | 3 ) comparisons in a graph. This is remarkable considering that there may be up to Ω ( | V | 2 ) edges in the graph, and every combination of edges is tested. It does so by incrementally improving an estimate on the shortest path between two vertices, until the estimate is optimal.

Consider a graph G with vertices V numbered 1 through  N . Further consider a function s h o r t e s t P a t h ( i , j , k ) that returns the shortest possible path from i to j using vertices only from the set { 1 , 2 , … , k } as intermediate points along the way. Now, given this function, our goal is to find the shortest path from each i to each j using only vertices in { 1 , 2 , … , k + 1 } .

For each of these pairs of vertices, the true shortest path could be either

(1) a path that only uses vertices in the set { 1 , … , k }

or

(2) a path that goes from i to k + 1 and then from k + 1 to j .

We know that the best path from i to j that only uses vertices 1 through k is defined by s h o r t e s t P a t h ( i , j , k ) , and it is clear that if there were a better path from i to k + 1 to j , then the length of this path would be the concatenation of the shortest path from i to k + 1 (using vertices in { 1 , … , k } ) and the shortest path from { k + 1 } to j (also using vertices in  { 1 , … , k } ).

If w ( i , j ) is the weight of the edge between vertices i and j , we can define s h o r t e s t P a t h ( i , j , k + 1 ) in terms of the following recursive formula: the base case is

s h o r t e s t P a t h ( i , j , 0 ) = w ( i , j )

and the recursive case is

s h o r t e s t P a t h ( i , j , k + 1 ) = m i n ( s h o r t e s t P a t h ( i , j , k ) , s h o r t e s t P a t h ( i , k + 1 , k ) + s h o r t e s t P a t h ( k + 1 , j , k ) ) .

This formula is the heart of the Floyd–Warshall algorithm. The algorithm works by first computing s h o r t e s t P a t h ( i , j , k ) for all ( i , j ) pairs for k = 1 , then k = 2 , etc. This process continues until k = N , and we have found the shortest path for all ( i , j ) pairs using any intermediate vertices. Pseudocode for this basic version follows:

1 let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity) 2 for each vertex v 3 dist[v][v] ← 0 4 for each edge (u,v) 5 dist[u][v] ← w(u,v) // the weight of the edge (u,v) 6 for k from 1 to |V| 7 for i from 1 to |V| 8 for j from 1 to |V| 9 if dist[i][j] > dist[i][k] + dist[k][j] 10 dist[i][j] ← dist[i][k] + dist[k][j] 11 end if

Example

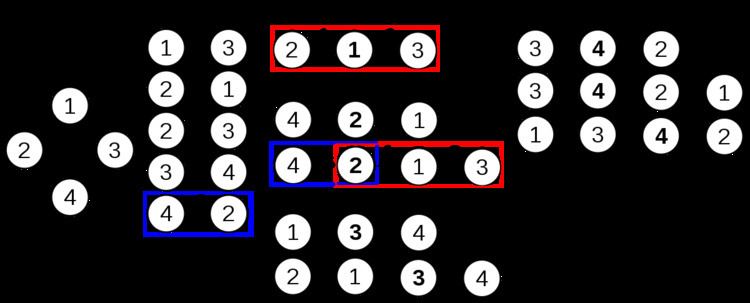
The algorithm above is executed on the graph on the left below:

Prior to the first iteration of the outer loop, labeled k = 0 above, the only known paths correspond to the single edges in the graph. At k = 1 , paths that go through the vertex 1 are found: in particular, the path [2,1,3] is found, replacing the path [2,3] which has fewer edges but is longer (in terms of weight). At k = 2 , paths going through the vertices {1,2} are found. The red and blue boxes show how the path [4,2,1,3] is assembled from the two known paths [4,2] and [2,1,3] encountered in previous iterations, with 2 in the intersection. The path [4,2,3] is not considered, because [2,1,3] is the shortest path encountered so far from 2 to 3. At k = 3 , paths going through the vertices {1,2,3} are found. Finally, at k = 4 , all shortest paths are found.

The distance matrix at each iteration of k , with the updated distances in bold, will be:

Behavior with negative cycles

A negative cycle is a cycle whose edges sum to a negative value. There is no shortest path between any pair of vertices i , j which form part of a negative cycle, because path-lengths from i to j can be arbitrarily small (negative). For numerically meaningful output, the Floyd–Warshall algorithm assumes that there are no negative cycles. Nevertheless, if there are negative cycles, the Floyd–Warshall algorithm can be used to detect them. The intuition is as follows:

The Floyd–Warshall algorithm iteratively revises path lengths between all pairs of vertices ( i , j ) , including where i = j ;

Initially, the length of the path ( i , i ) is zero;

A path [ i , k , … , i ] can only improve upon this if it has length less than zero, i.e. denotes a negative cycle;

Thus, after the algorithm, ( i , i ) will be negative if there exists a negative-length path from i back to i .

Hence, to detect negative cycles using the Floyd–Warshall algorithm, one can inspect the diagonal of the path matrix, and the presence of a negative number indicates that the graph contains at least one negative cycle. To avoid numerical problems one should check for negative numbers on the diagonal of the path matrix within the inner for loop of the algorithm. Obviously, in an undirected graph a negative edge creates a negative cycle (i.e., a closed walk) involving its incident vertices. Considering all edges of the above example graph as undirected, e.g. the vertex sequence 4 – 2 – 4 is a cycle with weight sum −2.

Path reconstruction

The Floyd–Warshall algorithm typically only provides the lengths of the paths between all pairs of vertices. With simple modifications, it is possible to create a method to reconstruct the actual path between any two endpoint vertices. While one may be inclined to store the actual path from each vertex to each other vertex, this is not necessary, and in fact, is very costly in terms of memory. Instead, the shortest-path tree can be calculated for each node in Θ ( | E | ) time using Θ ( | V | ) memory to store each tree which allows us to efficiently reconstruct a path from any two connected vertices.

let dist be a | V | × | V | array of minimum distances initialized to ∞ (infinity) let next be a | V | × | V | array of vertex indices initialized to null procedure FloydWarshallWithPathReconstruction () for each edge (u,v) dist[u][v] ← w(u,v) // the weight of the edge (u,v) next[u][v] ← v for k from 1 to |V| // standard Floyd-Warshall implementation for i from 1 to |V| for j from 1 to |V| if dist[i][j] > dist[i][k] + dist[k][j] then dist[i][j] ← dist[i][k] + dist[k][j] next[i][j] ← next[i][k] procedure Path(u, v) if next[u][v] = null then return [] path = [u] while u ≠ v u ← next[u][v] path.append(u) return path

Analysis

Let n be | V | , the number of vertices. To find all n 2 of s h o r t e s t P a t h ( i , j , k ) (for all i and j ) from those of s h o r t e s t P a t h ( i , j , k − 1 ) requires 2 n 2 operations. Since we begin with s h o r t e s t P a t h ( i , j , 0 ) = e d g e C o s t ( i , j ) and compute the sequence of n matrices s h o r t e s t P a t h ( i , j , 1 ) , s h o r t e s t P a t h ( i , j , 2 ) , … , s h o r t e s t P a t h ( i , j , n ) , the total number of operations used is n ⋅ 2 n 2 = 2 n 3 . Therefore, the complexity of the algorithm is Θ ( n 3 ) .

Applications and generalizations

The Floyd–Warshall algorithm can be used to solve the following problems, among others:

Shortest paths in directed graphs (Floyd's algorithm).

Transitive closure of directed graphs (Warshall's algorithm). In Warshall's original formulation of the algorithm, the graph is unweighted and represented by a Boolean adjacency matrix. Then the addition operation is replaced by logical conjunction (AND) and the minimum operation by logical disjunction (OR).

Finding a regular expression denoting the regular language accepted by a finite automaton (Kleene's algorithm, a closely related generalization of the Floyd–Warshall algorithm)

Inversion of real matrices (Gauss–Jordan algorithm)

Optimal routing. In this application one is interested in finding the path with the maximum flow between two vertices. This means that, rather than taking minima as in the pseudocode above, one instead takes maxima. The edge weights represent fixed constraints on flow. Path weights represent bottlenecks; so the addition operation above is replaced by the minimum operation.

Fast computation of Pathfinder networks.

Widest paths/Maximum bandwidth paths

Computing canonical form of difference bound matrices (DBMs)

Implementations

Implementations are available for many programming languages.

For C++, in the boost::graph library

For C#, at QuickGraph

For C#, at QuickGraphPCL (A fork of QuickGraph with better compatibility with projects using Portable Code Libraries.)

For Java, in the Apache Commons Graph library

For JavaScript, in the Cytoscape library

For MATLAB, in the Matlab_bgl package

For Perl, in the Graph module

For Python, in the SciPy library (module scipy.sparse.csgraph) or NetworkX library

For R, in package e1071

Comparison with other shortest path algorithms

The Floyd–Warshall algorithm is a good choice for computing paths between all pairs of vertices in dense graphs, in which most or all pairs of vertices are connected by edges. For sparse graphs with non-negative edge weights, a better choice is to use Dijkstra's algorithm from each possible starting vertex, since the running time of repeated Dijkstra ( O ( | V | 2 log ⁡ | V | ) using binary heaps) is better than the O ( | V | 3 ) running time of the Floyd–Warshall algorithm when | E | is significantly smaller than | V | 2 . For sparse graphs with negative edges but no negative cycles, Johnson's algorithm can be used, with the same asymptotic running time as the repeated Dijkstra approach.

There are also known algorithms using fast matrix multiplication to speed up all-pairs shortest path computation in dense graphs, but these typically make extra assumptions on the edge weights (such as requiring them to be small integers). In addition, because of the high constant factors in their running time, they would only provide a speedup over the Floyd–Warshall algorithm for very large graphs.