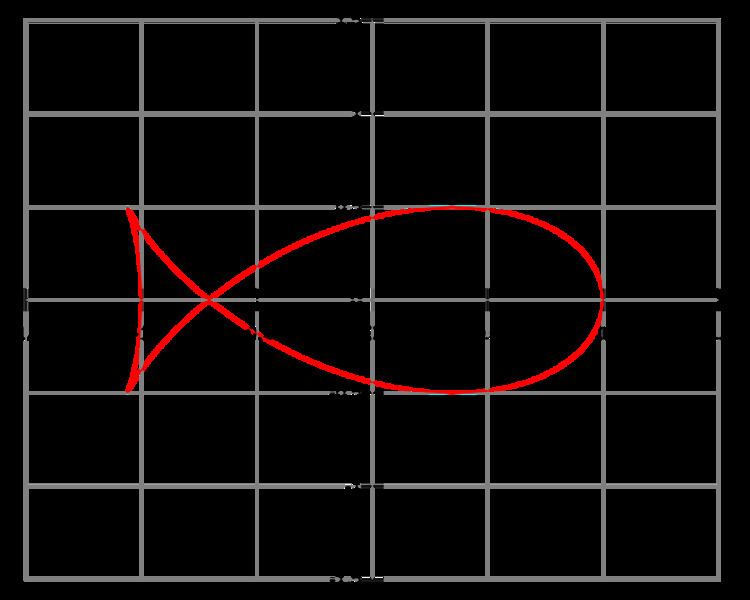
Fish curve - Alchetron, The Free Social Encyclopedia

A fish curve is an ellipse negative pedal curve that is shaped like a fish. In a fish curve, the pedal point is at the focus for the special case of the eccentricity e 2 = 1 2 . Fish curves can correspond to ellipses with parametric equations. In mathematics, parametric equations are a method of expressing a set of related quantities as explicit functions of a number of independent variables, known as "parameters." For example, rather than a function relating variables x and y in a Cartesian coordinate system such as y = f ( x ) , a parametric equation describes a position along the curve at time t by x = g ( t ) and y = h ( t ) . Then x and y are related to each other through their dependence on the parameter t. The fish curve is a kinematical example, using a time parameter to determine the position, velocity, and other information about a body in motion.

Equations

the corresponding fish curve has parametric equations:

x = a cos ⁡ ( t ) − a sin 2 ⁡ ( t ) 2 , y = a cos ⁡ ( t ) sin ⁡ ( t )

For an ellipse with the parametric equations:

x = a cos ⁡ ( t ) , y = a sin ⁡ ( t ) 2

and the Cartesian equation is:

− 2 a 4 2 a 3 x − 2 a 2 ( x 2 − 5 y 2 ) + ( 2 x 2 + y 2 ) 2 + 2 2 a x ( 2 x 2 − 3 y 2 ) + 2 a 2 ( y 2 − x 2 ) = 0 ,

which, when the origin is translated to the node, can be written as:

( 2 x 2 + y 2 ) 2 + 2 2 a x ( 2 x 2 − 3 y 2 ) + 2 a 2 ( y 2 − x 2 ) = 0

Area

The area of a fish curve is given by:

A = 1 2 | ∫ ( x y ′ − y x ′ ) d t |

= 1 8 a 2 | ∫ [ 3 cos ⁡ ( t ) + cos ⁡ ( 3 t ) + 2 2 sin 2 ⁡ ( t ) ] d t | ,

so the area of the tail and head are given by:

A T a i l = ( 2 3 − π 4 2 ) a 2

A H e a d = ( 2 3 + π 4 2 ) a 2

giving the overall area for the fish as:

A = 4 3 a 2 .

Curvature, arc length, and tangential angle

The arc length of the curve is given by a 2 ( 1 2 π + 3 ) .

The curvature of a fish curve is given by:

K ( t ) = 2 2 + 3 cos ⁡ ( t ) − cos ⁡ ( 3 t ) 2 a [ cos 4 ⁡ t + sin 2 ⁡ t + sin 4 ⁡ t + 2 sin ⁡ ( t ) sin ⁡ ( 2 t ) ] 3 2 ,

and the tangential angle is given by: ϕ ( t ) = π − arg ⁡ ( 2 − 1 − 2 ( 1 + 2 ) e i t − 1 )

where arg ⁡ ( z ) is the complex argument.

Conversion from two parametric equations to a single equation

Converting a set of parametric equations involves eliminating the variable t from the simultaneous equations x = x ( t ) , y = y ( t ) . If one of these equations can be solved for t, the expression obtained can be substituted into the other equation to obtain an equation involving x and y only. If x(t) and y(t) are rational functions then the techniques of the Theory of Equations such as resultants can be used to eliminate t. This is possible for the parametric equations describing the fish curve, as shown above.

Usefulness

The fish curve itself may not have any known applications to physical systems, but parametric equations in general do. Using parametric equations to express curves is practical as well as efficient; for example, one can integrate and differentiate such curves termwise. In general, a parametric curve is a function of one independent parameter, which is usually represented by t, while the symbols u and v are commonly used for parametric equations in two parameters.

References

Fish curve Wikipedia

(Text) CC BY-SA