Finite volume method in computational fluid dynamics is a discretization technique for partial differential equations that arise from physical conservation laws. These equations can be different in nature, e.g. elliptic, parabolic, or hyperbolic. First well-documented use was by Evans and Harlow (1957) at Los Alamos. The general equation for steady diffusion can be easily be derived from the general transport equation for property Φ by deleting transient and convective terms.
General Transport equation can be define as
∂ ρ ϕ ∂ t + div ( ρ ϕ υ ) = div ( Γ grad ϕ ) + S ϕ
where,
ρ is density and ϕ is conservative form of all fluid flow,
Γ is the Diffusion coefficient and S is the Source term.
div ( ρ ϕ υ ) is Net rate of flow of ϕ out of fluid element(convection),
div ( Γ grad ϕ ) is Rate of increase of ϕ due to diffusion,
S ϕ is Rate of increase of ϕ due to sources.
∂ ρ ϕ ∂ t is Rate of increase of ϕ of fluid element(transient),
Conditions under which the transient and convective terms goes to zero:
Steady StateLow Reynolds NumberFor one-dimensional steady state diffusion, General Transport equation reduces to:
or,
The following steps comprehend one-dimensional steady state diffusion -
STEP 1
Grid Generation
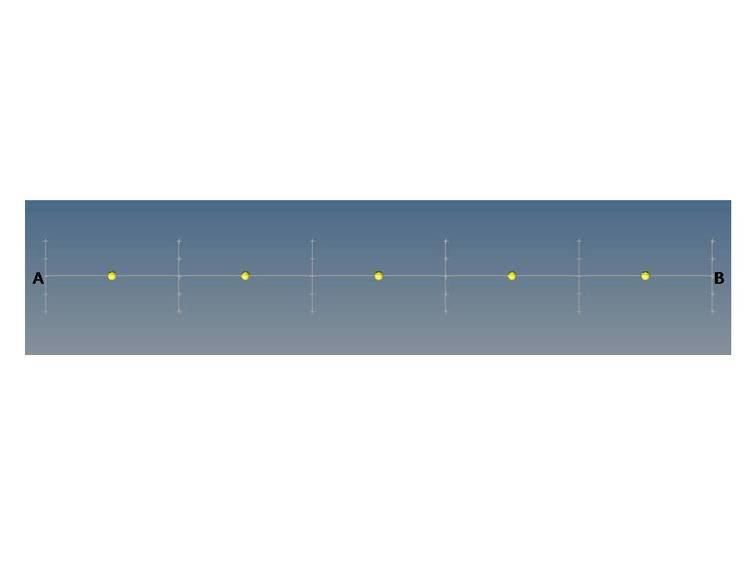
Divide the domain in equal parts of small domain.Place nodal points midway in between each small domain.
Create control volume using these nodal points.Create control volume near the edge in such a way that the physical boundaries coincide with control volume boundaries.(Figure 1)Assume a general nodal point 'P' for a general control volume.Adjacent nodal points in east and west are identified by E and W respectively.The west side face of the control volume is referred to by 'w' and east side control volume face by 'e'.(Figure 2)The distance between WP, wP, Pe and PE are identified by δ x W P , δ x w P , δ x P e and δ x P E respectively.(Figure 4)STEP 2
Discretization
The crux of Finite volume method is to integrate governing equation all over control volume, known discretization.Nodal points used to discretize equations.At nodal point P control volume is defined as (Figure 3)
∫ Δ V d d x ( Γ d ϕ d x ) d V + ∫ Δ V S d V = ( Γ A d ϕ d x ) e − ( Γ A d ϕ d x ) w + S → Δ V = 0
where
A is Cross-sectional Area Cross section (geometry) of control volume face, Δ V is Volume, S → is average value of source S over control volume
It states that diffusive flux Fick's laws of diffusion ϕ from east face minus west face leads to generation of flux in control volume. ϕ diffusive coefficient and d ϕ d x is required in order to interpreter useful conclusion.Central differencing technique [1] is used to derive ϕ diffusive coefficient.
Γ w = Γ W + Γ P 2
Γ w = Γ P + Γ E 2
d ϕ d x gradient from east to west is calculated with help of nodal points.(Figure 4) ( d ϕ d x ) e = ϕ E − ϕ P δ x P E ( d ϕ d x ) w = ϕ P − ϕ W δ x W P In practical situation source term can be linearize
S → Δ V = S u + S p ϕ p
Merging above equations leads to Γ e A e ( ϕ E − ϕ P δ x P E ) − Γ w A w ( ϕ P − ϕ W δ x P E ) + ( S u + S p ϕ p )
Re-arranging
( Γ e δ x P E A e + Γ w δ x W P A w − S p ) ϕ P = ( Γ w δ x W P A w ) ϕ W + ( Γ e δ x W P A e ) ϕ E + S u
Compare and identify above equation with
a P ϕ P = a W ϕ W + a E ϕ E + S u
where
STEP 3:
Solution of equations
Discretized equation must be set up at each of the nodal points in order to solve the problem.The resulting system of linear algebraic equation Linear equation is then solved to obtain distribution of the property ϕ at the nodal points by any form of matrix solution technique.The matrix of higher order [2] can be solved in MATLAB.This method can also be applied to a 2D situation. See Finite volume method for two dimensional diffusion problem.