Finite point method

History

Similar to other meshfree methods for PDEs, the finite point method (FPM) has its origins in techniques developed for scattered data fitting and interpolation, basically in the line of weighted least-squares methods (WLSQ). The latter can be regarded as particular forms of the moving least-squares method (MLS) proposed by Lancaster and Salkauskas. WLSQ methods have been widely used in meshfree techniques because allow retaining most of the MLS, but are more efficient and simple to implement. With these goals in mind, an outstanding investigation which led to the development of the FPM began in (Oñate, Idelsohn & Zienkiewicz, 1995a) and (Taylor, Zienkiewicz, Oñate & Idelsohn, 1995). The technique proposed was characterized by WLSQ approximations on local clouds of points and a equations discretization procedure based on point collocation (in the line of Batina’s works, 1989, 1992). The first applications of the FPM focused on adaptive compressible flow problems (Fischer, Onate & Idelsohn, 1995; Oñate, Idelsohn & Zienkiewicz, 1995a; Oñate, Idelsohn, Zienkiewicz & Fisher, 1995b). The effects on the approximation of the local clouds and weighting functions were also analyzed using linear and quadratic polynomial bases (Fischer, 1996). Additional studies in the context of convection-diffusion and incompressible flow problems gave the FPM a more solid base; cf. (Oñate, Idelsohn, Zienkiewicz & Taylor, 1996a) and (Oñate, Idelsohn, Zienkiewicz, Taylor & Sacco, 1996b). These works and (Oñate & Idelsohn, 1998) defined the basic FPM technique in use today.

Numerical approximation

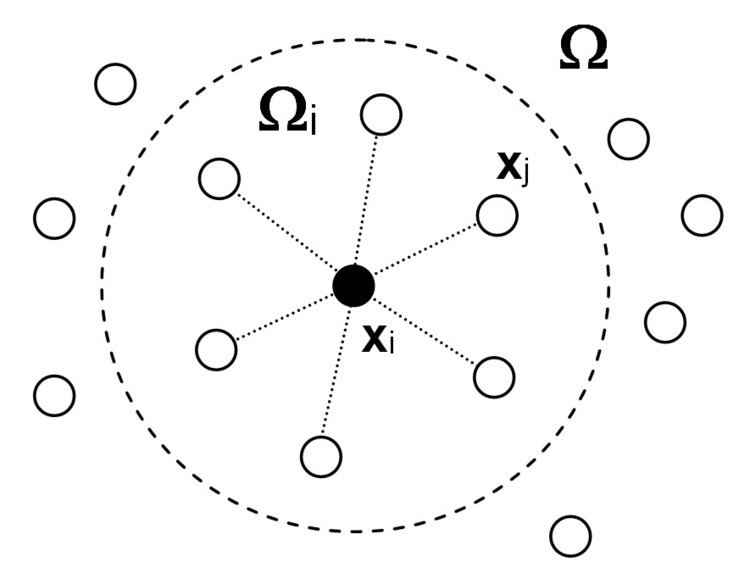
The approximation in the FPM can be summarized as follows. For each point x i in the analysis domain Ω (star point), an approximated solution is locally constructed by using a subset of surrounding supporting points x j , which belong to the problem domain (local cloud of points Ω i ). The approximation is computed as a linear combination of the cloud unknown nodal values (or parameters) and certain metric coefficients. These are obtained by solving a WLSQ problem at the cloud level, in which the distances between the nodal parameters and the approximated solution are minimized in a LSQ sense. Once the approximation metric coefficients are known, the problem governing PDEs are sampled at each star point by using a collocation method. The continuous variables (and their derivatives) are replaced in the sampled equations by the discrete approximated forms, and the solution of the resulting system allows calculating the unknown nodal values. Hence, the approximated solution satisfying the governing equations of the problem can be obtained. It is important to note that the highly local character of the FPM makes the method suitable for implementing efficient parallel solution schemes.

The construction of the typical FPM approximation is described in (Oñate & Idelsohn, 1998). An analysis of the approximation parameters can be found in (Ortega, Oñate & Idelsohn, 2007) and a more comprehensive study is conducted in (Ortega, 2014). Other approaches have also been proposed, see for instance (Boroomand, Tabatabaei and Oñate, 2005). An extension of the FPM approximation is presented in (Boroomand, Najjar & Oñate, 2009).

Fluid mechanics

The early lines of research and applications of the FPM to fluid flow problems are summarized in (Fischer, 1996). There, convective-diffusive problems were studied using LSQ and WLSQ polynomial approximations. The study focused on the effects of the cloud of points and weighting functions on the accuracy of the local approximation, which helped to understand the basic behavior of the FPM. The results showed that the 1D FPM approximation leads to discrete derivative forms similar to those obtained with central difference approximations, which are second-order accurate. However, the accuracy degrades to first-order for non-symmetric clouds, depending on the weighting function. Preliminary criteria about the selection of points conforming the local clouds were also defined with the aim to improve the ill-conditioning of the minimization problem. The flow solver employed in that work was based on a two-step Taylor-Galerkin scheme with explicit artificial dissipation. The numerical examples involved inviscid subsonic, transonic and supersonic two-dimensional problems, but a viscous low-Reynolds number test case was also provided. In general, the results obtained in this work were satisfactory and demonstrated that the introduction of weighting in the LSQ minimization leads to superior results (linear basis were used).

In a similar line of research, a residual stabilization technique derived in terms of flux balancing in a finite domain, known as Finite Increment Calculus (FIC) (Oñate, 1996, 1998), was introduced. The results were comparable to those obtained with explicit artificial dissipation, but with the advantage that the stabilization in FIC is introduced in a consistent manner, see (Oñate, Idelsohn, Zienkiewicz, Taylor & Sacco, 1996b) and (Oñate & Idelsohn, 1998a).

Among these developments, the issue of point generation was firstly addressed in (Löhner & Oñate, 1998). Based on an advancing front technique, the authors showed that point discretizations suitable for meshless computations can be generated more efficiently by avoiding the usual quality checks needed in conventional mesh generation. Highly competitive generation times were achieved in comparison with traditional meshers, showing for the first time that meshless methods are a feasible alternative to alleviate discretization problems.

Incompressible 2D flows were first studied in (Oñate, Sacco & Idelsohn, 2000) using a projection method stabilized through the FIC technique. A detailed analysis of this approach was carried out in (Sacco, 2002). Outstanding achievements from that work have given the FPM a more solid base; among them, the definition of local and normalized approximation bases, a procedure for constructing local clouds of points based on local Delaunay triangulation, and a criterion for evaluating the quality of the resultant approximation. The numerical applications presented focused mainly on two-dimensional (viscous and inviscid) incompressible flows, but a three-dimensional application example was also provided.

A preliminary application of the FPM in a Lagrangian framework, presented in (Idelsohn, Storti & Oñate, 2001), is also worth of mention. Despite the interesting results obtained for incompressible free surface flows, this line of research was not continued under the FPM and later formulations were exclusively based on Eulerian flow descriptions.

The first application of the FPM to the solution of 3D compressible flows was presented in a pioneer work by (Löhner, Sacco, Oñate & Idelsohn, 2002). There, a reliable and general procedure for constructing local clouds of points (based on a Delaunay technique) and a well-suited scheme for solving the flow equations were developed. In the solution scheme proposed, the discrete flux derivatives are written along edges connecting the cloud's points as a central difference-like expression plus an upwind biased term that provides convective stabilization. An approximate Riemann solver of Roe and van Leer flux vector splitting were used for this purpose. The approach proposed is more accurate (also more expensive) than artificial dissipation methods and, additionally, does not require the definition of geometrical measures in the local cloud and problem dependent parameters. The time integration of the equations was performed through a multi-stage explicit scheme in the line of Runge-Kutta methods.

Some years later, further research was carried out in relation to 3D FPM approximations in (Ortega, Oñate & Idelsohn, 2007). This work focused on constructing robust approximations regardless of the characteristics of the local support. To this end, local automatic adjusting of the weighting function and other approximation parameters were proposed. Further 3D applications of the method involved compressible aerodynamics flows with adaptive refinement (Ortega, Oñate & Idelsohn, 2009) and moving/deforming boundary problems (Ortega, Oñate & Idelsohn, 2013). In these works, the FPM showed satisfactory robustness and accuracy, and capabilities to address practical computations. Among other achievements, it was demonstrated that a complete regeneration of the model discretization could be an affordable solution strategy, even in large simulation problems. This result presents new possibilities for the meshless analysis of moving/deforming domain problems. The FPM was also applied with success to adaptive shallow water problems in (Ortega, Oñate, Idelsohn & Buachart, 2011) and (Buachart, Kanok-Nukulchai, Ortega & Oñate, 2014). A proposal to exploit meshless advantages in high-Reynolds viscous flow problems is presented in (Ortega, Oñate, Idelsohn & Flores, 2014a).

In the same field of applications, a major study on the accuracy, computational cost and parallel performance of the FPM was carried out in (Ortega, Oñate, Idelsohn & Flores, 2014b). There, the FPM was compared with an equivalent Finite Element-based solver, which provided a standard for assessing both, the characteristics of the meshless solver and its suitability to address practical applications. Some simplifications of the FPM technique were proposed in this work to improve efficiency and reduce the performance gap with FEM. Then, grid convergence studies using a wing-body configuration were conducted. The results showed comparable accuracy and performance, revealing the FPM competitive with respect to its FEM counterpart. This is important because meshless techniques are often considered impractical due to the poor efficiency of the initial implementations.

The FPM has also been applied in aeroacoustics in (Bajko, Cermak & Jicha, 2014). The solution scheme proposed is based on a linearized Riemann solver and successfully exploits the advantages of high-order FPM approximations. The results obtained are indicative of the potential of the FPM to address sound propagation problems.

Current lines of investigation

Current efforts are mainly oriented to exploit the capabilities of the FPM to work in parallel environments for solving large-scale practical problems, particularly in areas where meshless procedures can make useful contributions, for example problems involving complex geometry, moving/deforming domain, adaptive refinement and multiscale phenomena.