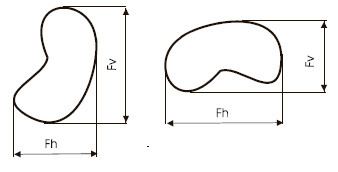
 | ||
The Feret diameter or Feret's diameter is a measure of an object size along a specified direction. In general, it can be defined as the distance between the two parallel planes restricting the object perpendicular to that direction. It is therefore also called the caliper diameter, referring to the measurement of the object size with a caliper. This measure is used in the analysis of particle sizes, for example in microscopy, where it is applied to projections of a three-dimensional (3D) object on a 2D plane. In such cases, the Feret diameter is defined as the distance between two parallel tangential lines rather than planes.
Contents
Mathematical properties
From Cauchy's theorem it follows that for a 2D convex body, the Feret diameter averaged over all directions (〈F〉) is equal to the ratio of the object perimeter (P) and pi, i.e., 〈F〉 = P/π. There is no such relation between 〈F〉 and P for a concave object.
Applications
Feret diameter is used in the analysis of particle size and its distribution, e.g. in a powder or a polycrystalline solid; Alternative measures include Martin diameter, Krumbein diameter and Heywood diameter. The term first became common in scientific literature in the 1970s.
It is also used in biology as a method to analyze the size of cells in tissue sections.
