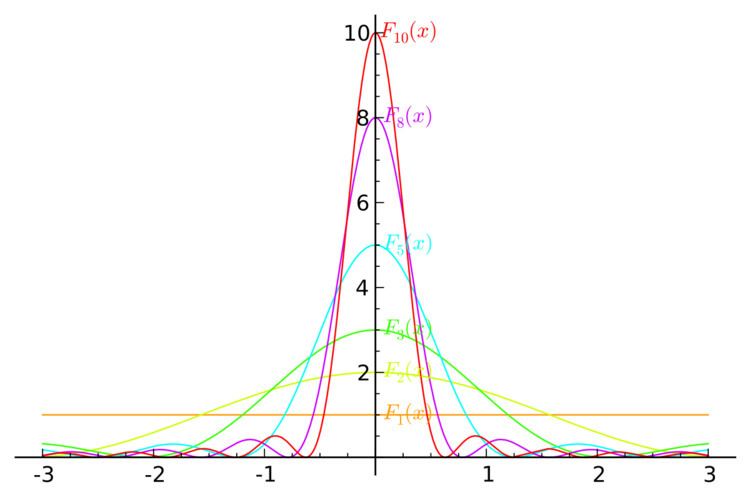
In mathematics, the Fejér kernel is a summability kernel used to express the effect of Cesàro summation on Fourier series. It is a non-negative kernel, giving rise to an approximate identity. It is named after the Hungarian mathematician Lipót Fejér (1880–1959).
The Fejér kernel is defined as
F n ( x ) = 1 n ∑ k = 0 n − 1 D k ( x ) , where
D k ( x ) = ∑ s = − k k e i s x is the kth order Dirichlet kernel. It can also be written in a closed form as
F n ( x ) = 1 n ( sin n x 2 sin x 2 ) 2 = 1 n ( 1 − cos ( n x ) 1 − cos x ) ,
where this expression is defined.
The Fejér kernel can also be expressed as
F n ( x ) = ∑ | j | ≤ n ( 1 − | j | n ) e i j x .
The Fejér kernel is a positive summability kernel. An important property of the Fejér kernel is F n ( x ) ≥ 0 with average value of 1 .
The convolution Fn is positive: for f ≥ 0 of period 2 π it satisfies
0 ≤ ( f ∗ F n ) ( x ) = 1 2 π ∫ − π π f ( y ) F n ( x − y ) d y . Since f ∗ D n = S n ( f ) = ∑ | j | ≤ n f ^ j e i j x , we have f ∗ F n = 1 n ∑ k = 0 n − 1 S k ( f ) , which is Cesàro summation of Fourier series.
By Young's inequality,
∥ F n ∗ f ∥ L p ( [ − π , π ] ) ≤ ∥ f ∥ L p ( [ − π , π ] ) for every
1 ≤ p ≤ ∞ for f ∈ L p .
Additionally, if f ∈ L 1 ( [ − π , π ] ) , then
f ∗ F n → f a.e.
Since [ − π , π ] is finite, L 1 ( [ − π , π ] ) ⊃ L 2 ( [ − π , π ] ) ⊃ ⋯ ⊃ L ∞ ( [ − π , π ] ) , so the result holds for other L p spaces, p ≥ 1 as well.
If f is continuous, then the convergence is uniform, yielding a proof of the Weierstrass theorem.
One consequence of the pointwise a.e. convergence is the uniquess of Fourier coefficients: If f , g ∈ L 1 with f ^ = g ^ , then f = g a.e. This follows from writing f ∗ F n = ∑ | j | ≤ n ( 1 − | j | n ) f ^ j e i j t , which depends only on the Fourier coefficients.A second consequence is that if lim n → ∞ S n ( f ) exists a.e., then lim n → ∞ F n ( f ) = f a.e., since Cesàro means F n ∗ f converge to the original sequence limit if it exists.