Harman Patil (Editor)

Factorization system

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Factorization system

In mathematics, it can be shown that every function can be written as the composite of a surjective function followed by an injective function. Factorization systems are a generalization of this situation in category theory.

Contents

Definition

A factorization system (E, M) for a category C consists of two classes of morphisms E and M of C such that:

  1. E and M both contain all isomorphisms of C and are closed under composition.
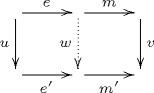
  2. Every morphism f of C can be factored as f = m ∘ e for some morphisms e ∈ E and m ∈ M .
  3. The factorization is functorial: if u and v are two morphisms such that v m e = m ′ e ′ u for some morphisms e , e ′ ∈ E and m , m ′ ∈ M , then there exists a unique morphism w making the following diagram commute:


Remark: ( u , v ) is a morphism from m e to m ′ e ′ in the arrow category.

Orthogonality

Two morphisms e and m are said to be orthogonal, denoted e ↓ m , if for every pair of morphisms u and v such that v e = m u there is a unique morphism w such that the diagram

commutes. This notion can be extended to define the orthogonals of sets of morphisms by

H ↑ = { e | ∀ h ∈ H , e ↓ h } and H ↓ = { m | ∀ h ∈ H , h ↓ m } .

Since in a factorization system E ∩ M contains all the isomorphisms, the condition (3) of the definition is equivalent to

(3') E ⊂ M ↑ and M ⊂ E ↓ .


Proof: In the previous diagram (3), take m := i d ,   e ′ := i d (identity on the appropriate object) and m ′ := m .

Equivalent definition

The pair ( E , M ) of classes of morphisms of C is a factorization system if and only if it satisfies the following conditions:

  1. Every morphism f of C can be factored as f = m ∘ e with e ∈ E and m ∈ M .
  2. E = M ↑ and M = E ↓ .

Weak factorization systems

Suppose e and m are two morphisms in a category C. Then e has the left lifting property with respect to m (resp. m has the right lifting property with respect to e) when for every pair of morphisms u and v such that ve=mu there is a morphism w such that the following diagram commutes. The difference with orthogonality is that w is not necessarily unique.

A weak factorization system (E, M) for a category C consists of two classes of morphisms E and M of C such that :

  1. The class E is exactly the class of morphisms having the left lifting property wrt the morphisms of M.
  2. The class M is exactly the class of morphisms having the right lifting property wrt the morphisms of E.
  3. Every morphism f of C can be factored as f = m ∘ e for some morphisms e ∈ E and m ∈ M .

References

Factorization system Wikipedia
(Text) CC BY-SA