In mathematics, more specifically in topological groups, an extension of topological groups, or a topological extension, is a short exact sequence 0 → H → ı X → π G → 0 where H , X and G are topological groups and i and π are continuous homomorphisms which are also open onto their images. Every extension of topological group is therefore a group extension
We say that the topological extensions
0 → H → i X → π G → 0 and
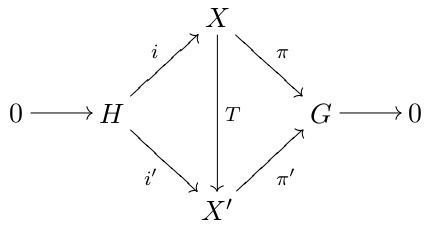
0 → H → i ′ X ′ → π ′ G → 0 are equivalent (or congruent) if there exists a topological isomorphism T : X → X ′ making commutative the diagram of Figure 1.
We say that the topological extension
0 → H → i X → π G → 0 is a split extension (or splits) if it is equivalent to the trivial extension
0 → H → i H H × G → π G G → 0 where i H : H → H × G is the natural inclusion over the first factor and π G : H × G → G is the natural projection over the second factor.
It is easy to prove that the topological extension 0 → H → i X → π G → 0 splits if and only if there is a continuous homomorphism R : X → H such that R ∘ i is the identity map on H
Note that the topological extension 0 → H → i X → π G → 0 splits if and only if the subgroup i ( H ) is a topological direct summand of X
Take R the real numbers and Z the integer numbers. Take ı the natural inclusion and π the natural projection. Thenis an extension of topological abelian groups. Indeed it is an example of a non-splitting extension.
An extension of topological abelian groups will be a short exact sequence 0 → H → ı X → π G → 0 where H , X and G are locally compact abelian groups and i and π are relatively open continuous homomorphisms.
Let be an extension of locally compact abelian groupsTake
H ∧ , X ∧ and
G ∧ the
Pontryagin duals of
H , X and
G and take
i ∧ and
π ∧ the dual maps of
i and
π . Then the sequence
0 → G ∧ → π ∧ X ∧ → ı ∧ H ∧ → 0 is an extension of locally compact abelian groups.